Computer-Aided Design of Rational Motions for 4R and 6R Spatial Mechanism Synthesis

This paper focuses on geometric methods for generating rational motions used in the design of single-loop rational linkages, 1-degree-of-freedom mechanisms that can execute prescribed spatial tasks. Building on established rational motion synthesis methods, we introduce a new interpolation scheme for seven 3D points based on cubic quaternionic Bezier curves. The resulting motion admits factorization, i.e. the synthesis of a spatial six-bar mechanism whose tool frame passes the specified seven points. To support engineering practice, we provide open-source CAD tools that implement also the other methods and provide fast visual evaluation of motion generation and mechanism synthesis.

Rational Linkages: From Poses to 3D-printed Prototypes

In this paper, a set of tools is introduced that simplifies the synthesis and rapid-prototyping of single-loop rational kinematic chains. It allows the user to perform rational motion interpolation of up to four given poses and yields the design parameters of a linkage that can execute this motion. The package also provides a visualization of the output and performs a self-collision analysis with the possibility to adapt the design parameters. The results can be imported into CAD-systems for fast 3D printing.

An Overconstrained Vertical Darboux Mechanism

In this article, we will construct an overconstrained closed-loop linkage consisting of four revolute and one cylindrical joint. It is obtained by factorization of a prescribed vertical Darboux motion. We will investigate the kinematic behaviour of the obtained mechanism, which turns out to have multiple operation modes. Under certain conditions on the design parameters, two of the operation modes will correspond to vertical Darboux motions. It turns out, that for these design parameters, there also exists a second assembly mode.

Analysis of a 3-RUU Parallel Manipulator

The aim of this paper is to give a detailed examination of the input and output singularities of a 3-RUU parallel manipulator in the translational operation mode. This task is achieved by using algebraic constraint equations. For this type of manipulator a complete workspace representation in Study coordinates is presented after elimination of the input parameters. Both, input and output singularities are mapped into a Study subspace as well as into the joint space. Therewith a detailed singularity investigation of the translational operation mode of a 3-RUU parallel manipulator is provided. This paper is an extended version of a previous publication. The addendum comprises the discovery of a possible transition between two operation modes as well as a self motion and an examination of another component of the output singularity surface, most of them for arbitrary design parameters.

Rational Motions with Generic Trajectories of Low Degree

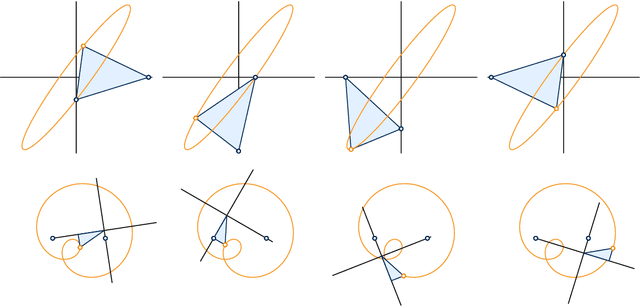
The trajectories of a rational motion given by a polynomial of degree n in the dual quaternion model of rigid body displacements are generically of degree 2n. In this article we study those exceptional motions whose trajectory degree is lower. An algebraic criterion for this drop of degree is existence of certain right factors, a geometric criterion involves one of two families of rulings on an invariant quadric. Our characterizations allow the systematic construction of rational motions with exceptional degree reduction and explain why the trajectory degrees of a rational motion and its inverse motion can be different.