Hanbang Liang
Diffusion Restoration Adapter for Real-World Image Restoration
Feb 28, 2025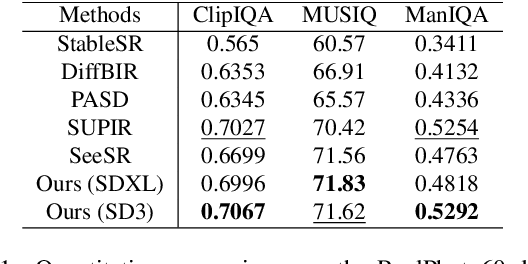
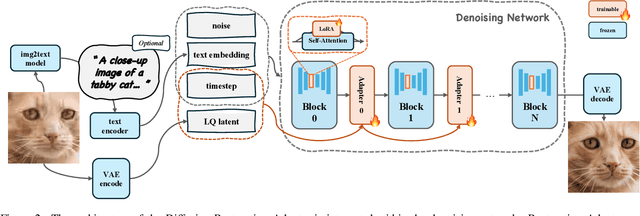
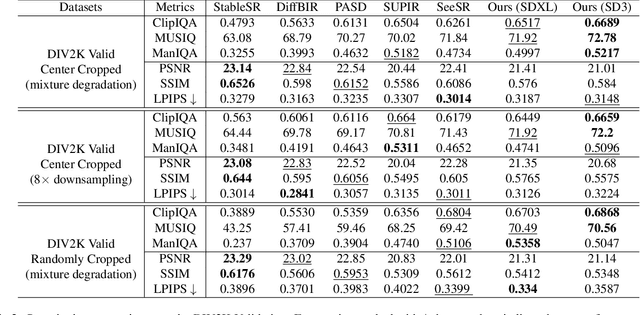
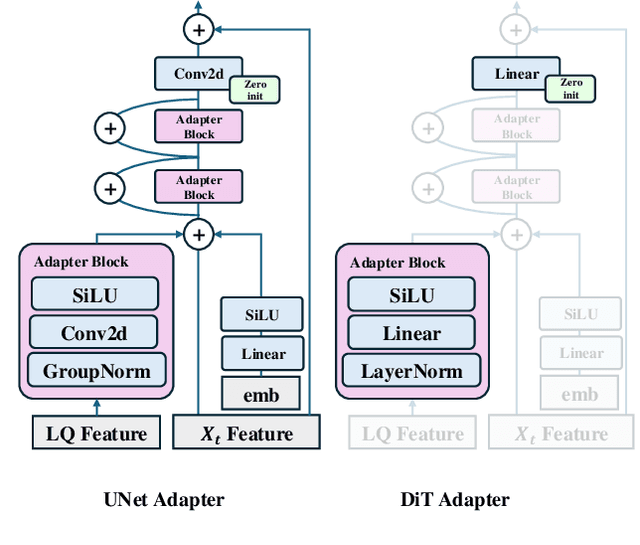
Abstract:Diffusion models have demonstrated their powerful image generation capabilities, effectively fitting highly complex image distributions. These models can serve as strong priors for image restoration. Existing methods often utilize techniques like ControlNet to sample high quality images with low quality images from these priors. However, ControlNet typically involves copying a large part of the original network, resulting in a significantly large number of parameters as the prior scales up. In this paper, we propose a relatively lightweight Adapter that leverages the powerful generative capabilities of pretrained priors to achieve photo-realistic image restoration. The Adapters can be adapt to both denoising UNet and DiT, and performs excellent.
Combating Mode Collapse in GANs via Manifold Entropy Estimation
Aug 25, 2022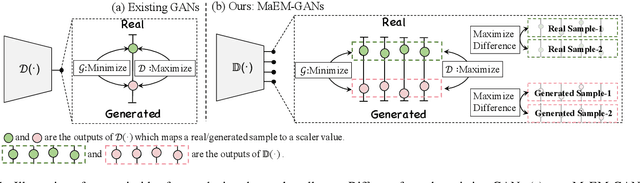
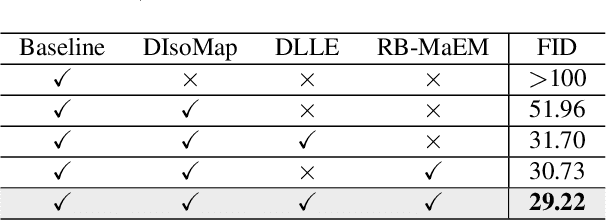
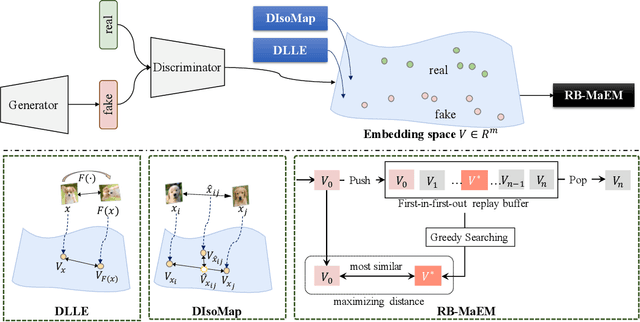
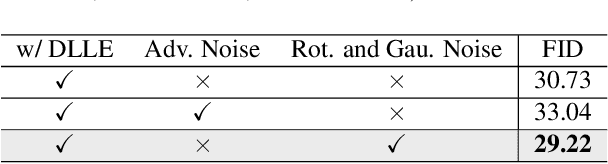
Abstract:Generative Adversarial Networks (GANs) have shown compelling results in various tasks and applications in recent years. However, mode collapse remains a critical problem in GANs. In this paper, we propose a novel training pipeline to address the mode collapse issue of GANs. Different from existing methods, we propose to generalize the discriminator as feature embedding, and maximize the entropy of distributions in the embedding space learned by the discriminator. Specifically, two regularization terms, i.e.Deep Local Linear Embedding (DLLE) and Deep Isometric feature Mapping (DIsoMap), are designed to encourage the discriminator to learn the structural information embedded in the data, such that the embedding space learned by the discriminator can be well formed. Based on the well-learned embedding space supported by the discriminator, a non-parametric entropy estimator is designed to efficiently maximize the entropy of embedding vectors, playing as an approximation of maximizing the entropy of the generated distribution. Through improving the discriminator and maximizing the distance of the most similar samples in the embedding space, our pipeline effectively reduces the mode collapse without sacrificing the quality of generated samples. Extensive experimental results show the effectiveness of our method which outperforms the GAN baseline, MaF-GAN on CelebA (9.13 vs. 12.43 in FID) and surpasses the recent state-of-the-art energy-based model on the ANIME-FACE dataset (2.80 vs. 2.26 in Inception score).
Manifold-preserved GANs
Sep 18, 2021
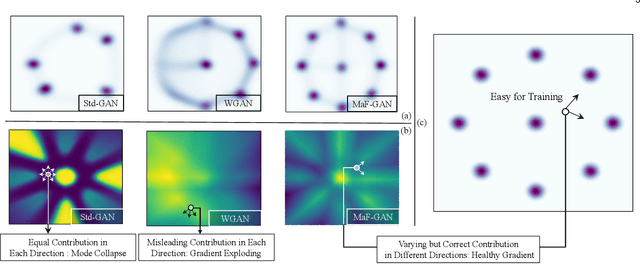
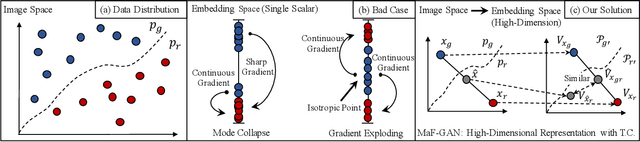
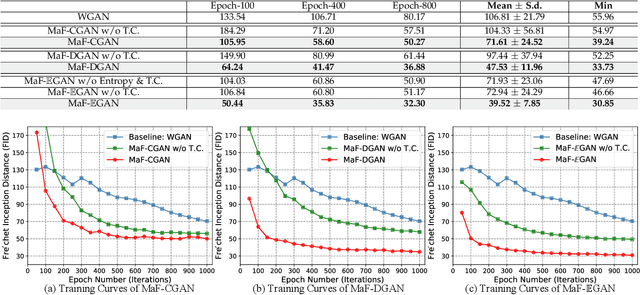
Abstract:Generative Adversarial Networks (GANs) have been widely adopted in various fields. However, existing GANs generally are not able to preserve the manifold of data space, mainly due to the simple representation of discriminator for the real/generated data. To address such open challenges, this paper proposes Manifold-preserved GANs (MaF-GANs), which generalize Wasserstein GANs into high-dimensional form. Specifically, to improve the representation of data, the discriminator in MaF-GANs is designed to map data into a high-dimensional manifold. Furthermore, to stabilize the training of MaF-GANs, an operation with precise and universal solution for any K-Lipschitz continuity, called Topological Consistency is proposed. The effectiveness of the proposed method is justified by both theoretical analysis and empirical results. When adopting DCGAN as the backbone on CelebA (256*256), the proposed method achieved 12.43 FID, which outperforms the state-of-the-art model like Realness GAN (23.51 FID) by a large margin. Code will be made publicly available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge