Manifold-preserved GANs
Paper and Code
Sep 18, 2021
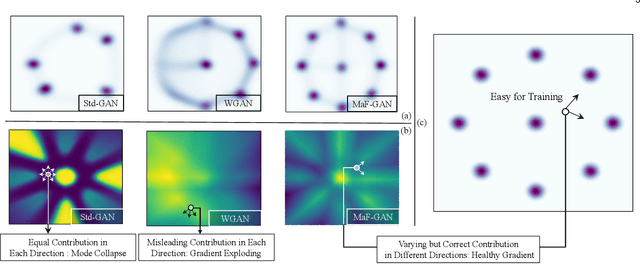
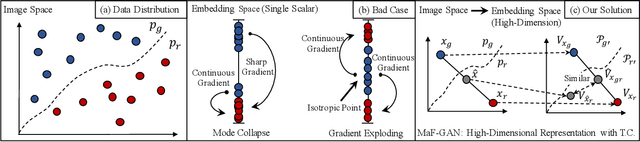
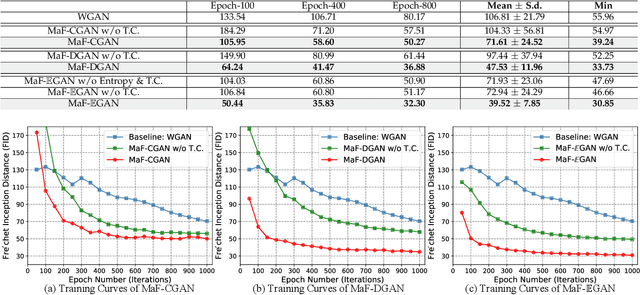
Generative Adversarial Networks (GANs) have been widely adopted in various fields. However, existing GANs generally are not able to preserve the manifold of data space, mainly due to the simple representation of discriminator for the real/generated data. To address such open challenges, this paper proposes Manifold-preserved GANs (MaF-GANs), which generalize Wasserstein GANs into high-dimensional form. Specifically, to improve the representation of data, the discriminator in MaF-GANs is designed to map data into a high-dimensional manifold. Furthermore, to stabilize the training of MaF-GANs, an operation with precise and universal solution for any K-Lipschitz continuity, called Topological Consistency is proposed. The effectiveness of the proposed method is justified by both theoretical analysis and empirical results. When adopting DCGAN as the backbone on CelebA (256*256), the proposed method achieved 12.43 FID, which outperforms the state-of-the-art model like Realness GAN (23.51 FID) by a large margin. Code will be made publicly available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge