Rotation Invariant Quantization for Model Compression

Post-training Neural Network (NN) model compression is an attractive approach for deploying large, memory-consuming models on devices with limited memory resources. In this study, we investigate the rate-distortion tradeoff for NN model compression. First, we suggest a Rotation-Invariant Quantization (RIQ) technique that utilizes a single parameter to quantize the entire NN model, yielding a different rate at each layer, i.e., mixed-precision quantization. Then, we prove that our rotation-invariant approach is optimal in terms of compression. We rigorously evaluate RIQ and demonstrate its capabilities on various models and tasks. For example, RIQ facilitates $\times 19.4$ and $\times 52.9$ compression ratios on pre-trained VGG dense and pruned models, respectively, with $<0.4\%$ accuracy degradation. Code: \url{https://github.com/ehaleva/RIQ}.

Demonstration Informed Specification Search

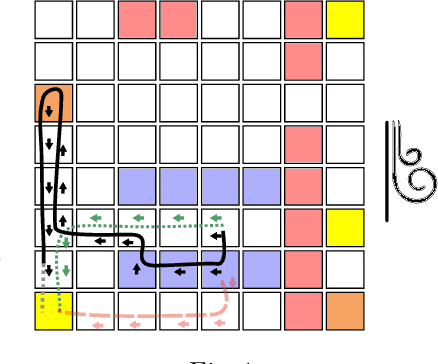
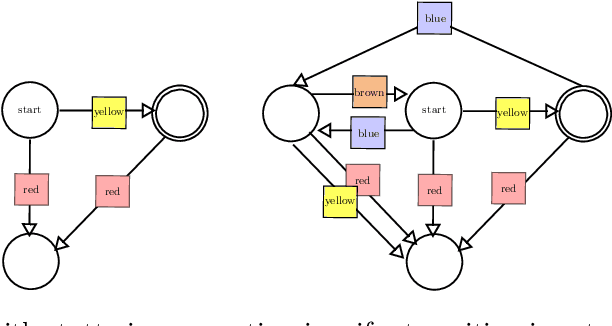
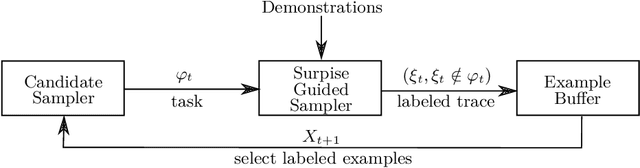
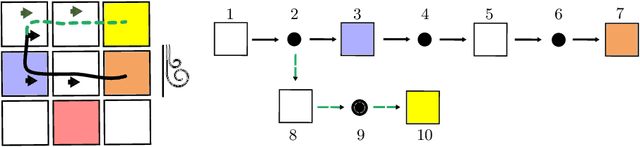
This paper considers the problem of learning history dependent task specifications, e.g. automata and temporal logic, from expert demonstrations. Unfortunately, the (countably infinite) number of tasks under consideration combined with an a-priori ignorance of what historical features are needed to encode the demonstrated task makes existing approaches to learning tasks from demonstrations inapplicable. To address this deficit, we propose Demonstration Informed Specification Search (DISS): a family of algorithms parameterized by black box access to (i) a maximum entropy planner and (ii) an algorithm for identifying concepts, e.g., automata, from labeled examples. DISS works by alternating between (i) conjecturing labeled examples to make the demonstrations less surprising and (ii) sampling concepts consistent with the current labeled examples. In the context of tasks described by deterministic finite automata, we provide a concrete implementation of DISS that efficiently combines partial knowledge of the task and a single expert demonstration to identify the full task specification.

Learning Branching Heuristics for Propositional Model Counting

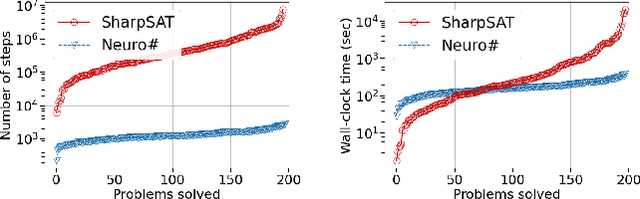
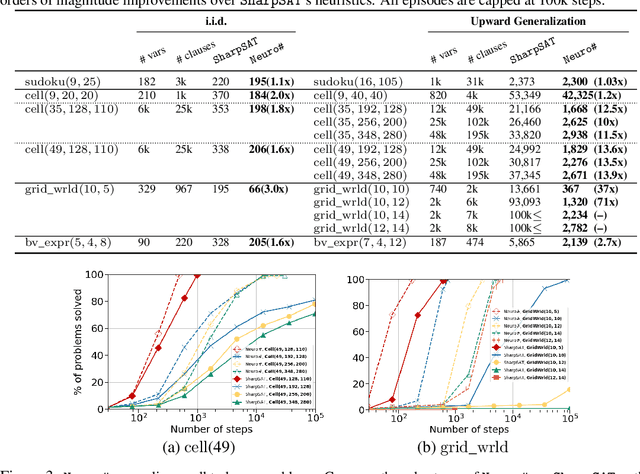
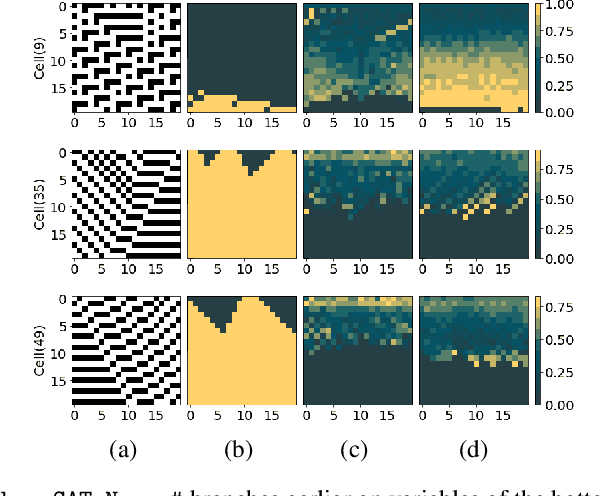
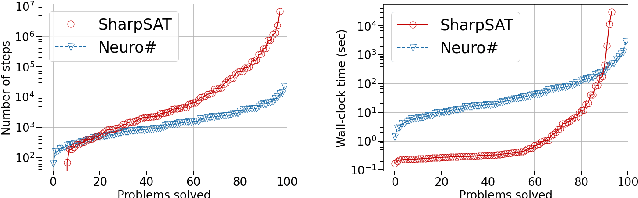
Propositional model counting or #SAT is the problem of computing the number of satisfying assignments of a Boolean formula and many discrete probabilistic inference problems can be translated into a model counting problem to be solved by #SAT solvers. Generic ``exact'' #SAT solvers, however, are often not scalable to industrial-level instances. In this paper, we present Neuro#, an approach for learning branching heuristics for exact #SAT solvers via evolution strategies (ES) to reduce the number of branching steps the solver takes to solve an instance. We experimentally show that our approach not only reduces the step count on similarly distributed held-out instances but it also generalizes to much larger instances from the same problem family. The gap between the learned and the vanilla solver on larger instances is sometimes so wide that the learned solver can even overcome the run time overhead of querying the model and beat the vanilla in wall-clock time by orders of magnitude.

Learning Heuristics for Automated Reasoning through Deep Reinforcement Learning

We demonstrate how to learn efficient heuristics for automated reasoning algorithms through deep reinforcement learning. We consider search algorithms for quantified Boolean logics, that already can solve formulas of impressive size - up to 100s of thousands of variables. The main challenge is to find a representation which lends to making predictions in a scalable way. The heuristics learned through our approach significantly improve over the handwritten heuristics for several sets of formulas.