Learning Branching Heuristics for Propositional Model Counting

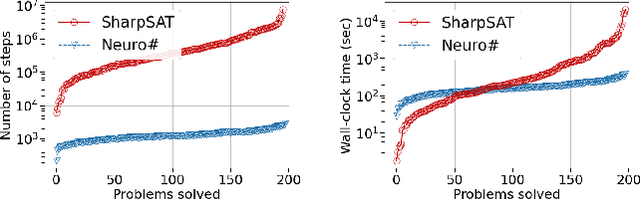
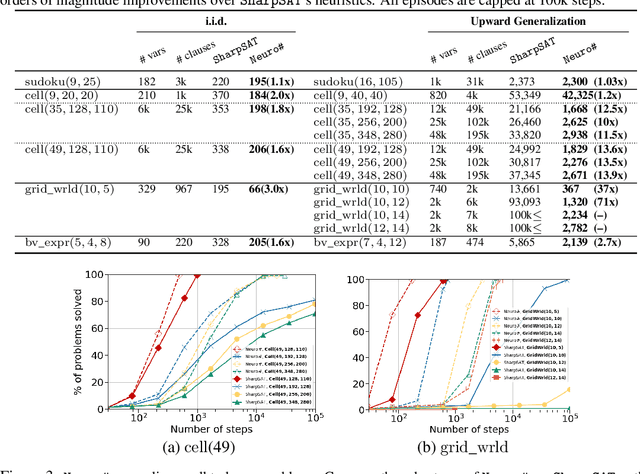
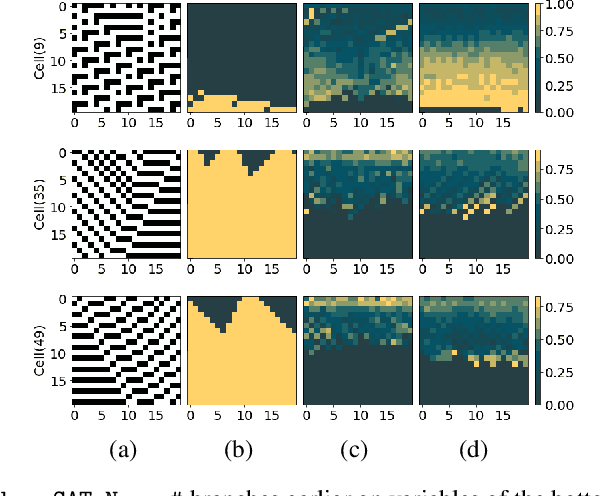
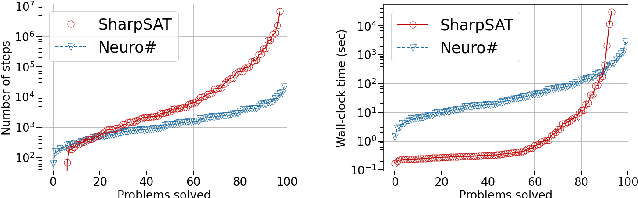
Propositional model counting or #SAT is the problem of computing the number of satisfying assignments of a Boolean formula and many discrete probabilistic inference problems can be translated into a model counting problem to be solved by #SAT solvers. Generic ``exact'' #SAT solvers, however, are often not scalable to industrial-level instances. In this paper, we present Neuro#, an approach for learning branching heuristics for exact #SAT solvers via evolution strategies (ES) to reduce the number of branching steps the solver takes to solve an instance. We experimentally show that our approach not only reduces the step count on similarly distributed held-out instances but it also generalizes to much larger instances from the same problem family. The gap between the learned and the vanilla solver on larger instances is sometimes so wide that the learned solver can even overcome the run time overhead of querying the model and beat the vanilla in wall-clock time by orders of magnitude.