The establishment of static digital humans and the integration with spinal models

Adolescent idiopathic scoliosis (AIS), a prevalent spinal deformity, significantly affects individuals' health and quality of life. Conventional imaging techniques, such as X - rays, computed tomography (CT), and magnetic resonance imaging (MRI), offer static views of the spine. However, they are restricted in capturing the dynamic changes of the spine and its interactions with overall body motion. Therefore, developing new techniques to address these limitations has become extremely important. Dynamic digital human modeling represents a major breakthrough in digital medicine. It enables a three - dimensional (3D) view of the spine as it changes during daily activities, assisting clinicians in detecting deformities that might be missed in static imaging. Although dynamic modeling holds great potential, constructing an accurate static digital human model is a crucial initial step for high - precision simulations. In this study, our focus is on constructing an accurate static digital human model integrating the spine, which is vital for subsequent dynamic digital human research on AIS. First, we generate human point - cloud data by combining the 3D Gaussian method with the Skinned Multi - Person Linear (SMPL) model from the patient's multi - view images. Then, we fit a standard skeletal model to the generated human model. Next, we align the real spine model reconstructed from CT images with the standard skeletal model. We validated the resulting personalized spine model using X - ray data from six AIS patients, with Cobb angles (used to measure the severity of scoliosis) as evaluation metrics. The results indicate that the model's error was within 1 degree of the actual measurements. This study presents an important method for constructing digital humans.

Dual-Frequency Filtering Self-aware Graph Neural Networks for Homophilic and Heterophilic Graphs

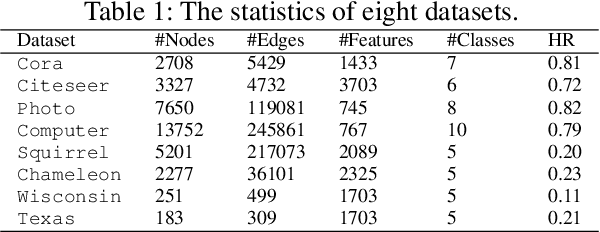
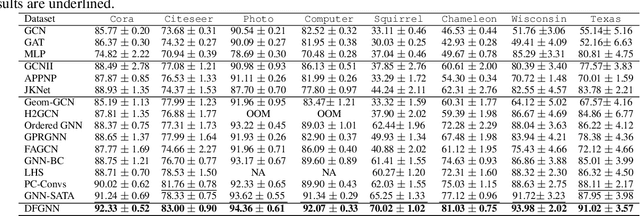
Graph Neural Networks (GNNs) have excelled in handling graph-structured data, attracting significant research interest. However, two primary challenges have emerged: interference between topology and attributes distorting node representations, and the low-pass filtering nature of most GNNs leading to the oversight of valuable high-frequency information in graph signals. These issues are particularly pronounced in heterophilic graphs. To address these challenges, we propose Dual-Frequency Filtering Self-aware Graph Neural Networks (DFGNN). DFGNN integrates low-pass and high-pass filters to extract smooth and detailed topological features, using frequency-specific constraints to minimize noise and redundancy in the respective frequency bands. The model dynamically adjusts filtering ratios to accommodate both homophilic and heterophilic graphs. Furthermore, DFGNN mitigates interference by aligning topological and attribute representations through dynamic correspondences between their respective frequency bands, enhancing overall model performance and expressiveness. Extensive experiments conducted on benchmark datasets demonstrate that DFGNN outperforms state-of-the-art methods in classification performance, highlighting its effectiveness in handling both homophilic and heterophilic graphs.

Vectorial Dimension Reduction for Tensors Based on Bayesian Inference

Dimensionality reduction for high-order tensors is a challenging problem. In conventional approaches, higher order tensors are `vectorized` via Tucker decomposition to obtain lower order tensors. This will destroy the inherent high-order structures or resulting in undesired tensors, respectively. This paper introduces a probabilistic vectorial dimensionality reduction model for tensorial data. The model represents a tensor by employing a linear combination of same order basis tensors, thus it offers a mechanism to directly reduce a tensor to a vector. Under this expression, the projection base of the model is based on the tensor CandeComp/PARAFAC (CP) decomposition and the number of free parameters in the model only grows linearly with the number of modes rather than exponentially. A Bayesian inference has been established via the variational EM approach. A criterion to set the parameters (factor number of CP decomposition and the number of extracted features) is empirically given. The model outperforms several existing PCA-based methods and CP decomposition on several publicly available databases in terms of classification and clustering accuracy.

Mixture of Bilateral-Projection Two-dimensional Probabilistic Principal Component Analysis

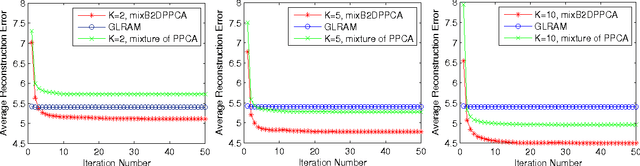
The probabilistic principal component analysis (PPCA) is built upon a global linear mapping, with which it is insufficient to model complex data variation. This paper proposes a mixture of bilateral-projection probabilistic principal component analysis model (mixB2DPPCA) on 2D data. With multi-components in the mixture, this model can be seen as a soft cluster algorithm and has capability of modeling data with complex structures. A Bayesian inference scheme has been proposed based on the variational EM (Expectation-Maximization) approach for learning model parameters. Experiments on some publicly available databases show that the performance of mixB2DPPCA has been largely improved, resulting in more accurate reconstruction errors and recognition rates than the existing PCA-based algorithms.