Reinforcement Learning for Robust Athletic Intelligence: Lessons from the 2nd 'AI Olympics with RealAIGym' Competition

In the field of robotics many different approaches ranging from classical planning over optimal control to reinforcement learning (RL) are developed and borrowed from other fields to achieve reliable control in diverse tasks. In order to get a clear understanding of their individual strengths and weaknesses and their applicability in real world robotic scenarios is it important to benchmark and compare their performances not only in a simulation but also on real hardware. The '2nd AI Olympics with RealAIGym' competition was held at the IROS 2024 conference to contribute to this cause and evaluate different controllers according to their ability to solve a dynamic control problem on an underactuated double pendulum system with chaotic dynamics. This paper describes the four different RL methods submitted by the participating teams, presents their performance in the swing-up task on a real double pendulum, measured against various criteria, and discusses their transferability from simulation to real hardware and their robustness to external disturbances.

Quantum Deep Reinforcement Learning for Robot Navigation Tasks

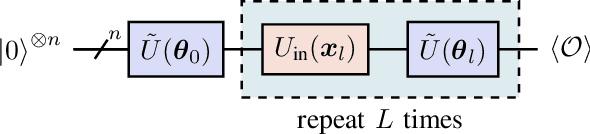
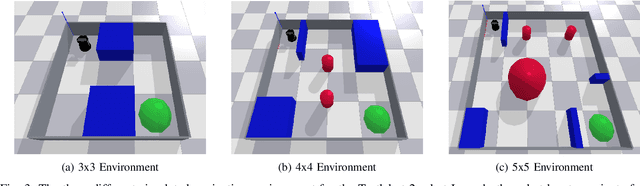
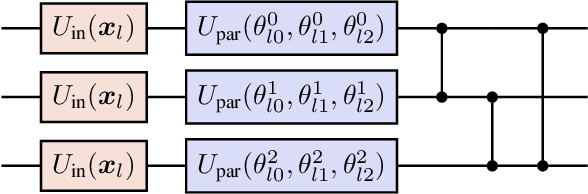
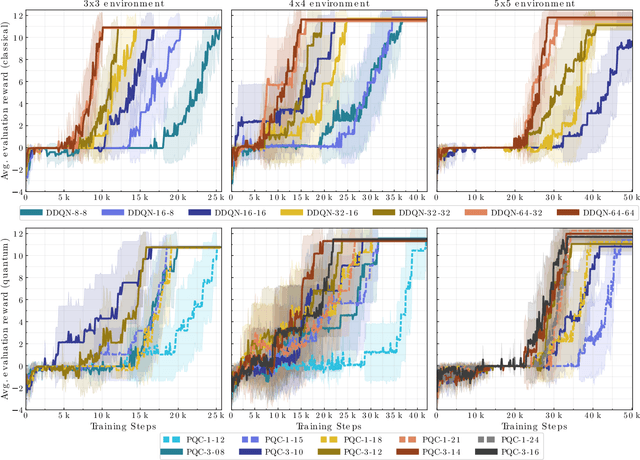
In this work, we utilize Quantum Deep Reinforcement Learning as method to learn navigation tasks for a simple, wheeled robot in three simulated environments of increasing complexity. We show similar performance of a parameterized quantum circuit trained with well established deep reinforcement learning techniques in a hybrid quantum-classical setup compared to a classical baseline. To our knowledge this is the first demonstration of quantum machine learning (QML) for robotic behaviors. Thus, we establish robotics as a viable field of study for QML algorithms and henceforth quantum computing and quantum machine learning as potential techniques for future advancements in autonomous robotics. Beyond that, we discuss current limitations of the presented approach as well as future research directions in the field of quantum machine learning for autonomous robots.

A Development Cycle for Automated Self-Exploration of Robot Behaviors

In this paper we introduce Q-Rock, a development cycle for the automated self-exploration and qualification of robotic behaviors. With Q-Rock, we suggest a novel, integrative approach to automate robot development processes. Q-Rock combines several machine learning and reasoning techniques to deal with the increasing complexity in the design of robotic systems. The Q-Rock development cycle consists of three complementary processes: (1) automated exploration of capabilities that a given robotic hardware provides, (2) classification and semantic annotation of these capabilities to generate more complex behaviors, and (3) mapping between application requirements and available behaviors. These processes are based on a graph-based representation of a robot's structure, including hardware and software components. A graph-database serves as central, scalable knowledge base to enable collaboration with robot designers including mechanical and electrical engineers, software developers and machine learning experts. In this paper we formalize Q-Rock's integrative development cycle and highlight its benefits with a proof-of-concept implementation and a use case demonstration.

Combinatorics of a Discrete Trajectory Space for Robot Motion Planning

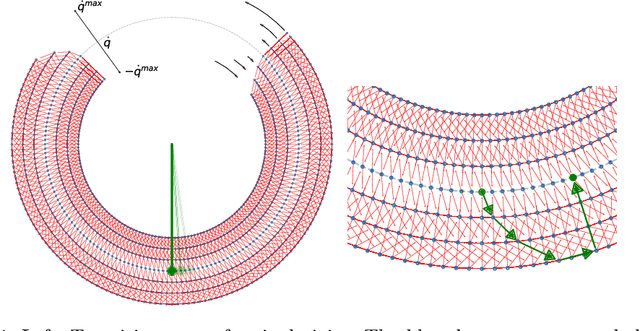
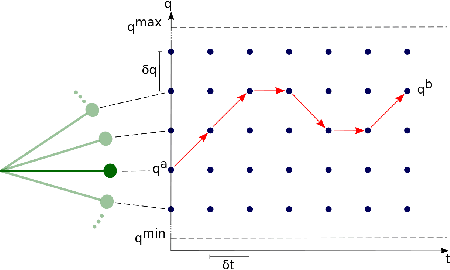
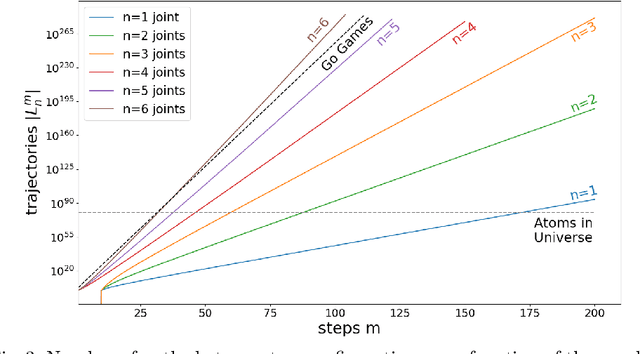
Motion planning is a difficult problem in robot control. The complexity of the problem is directly related to the dimension of the robot's configuration space. While in many theoretical calculations and practical applications the configuration space is modeled as a continuous space, we present a discrete robot model based on the fundamental hardware specifications of a robot. Using lattice path methods, we provide estimates for the complexity of motion planning by counting the number of possible trajectories in a discrete robot configuration space.