Sparsity aware coding for single photon sensitive vision using Selective Sensing

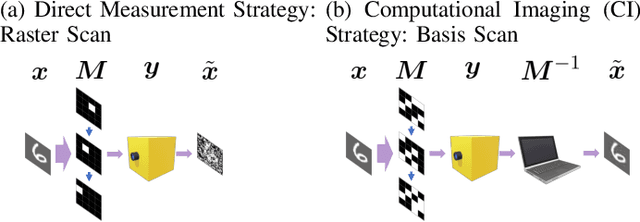
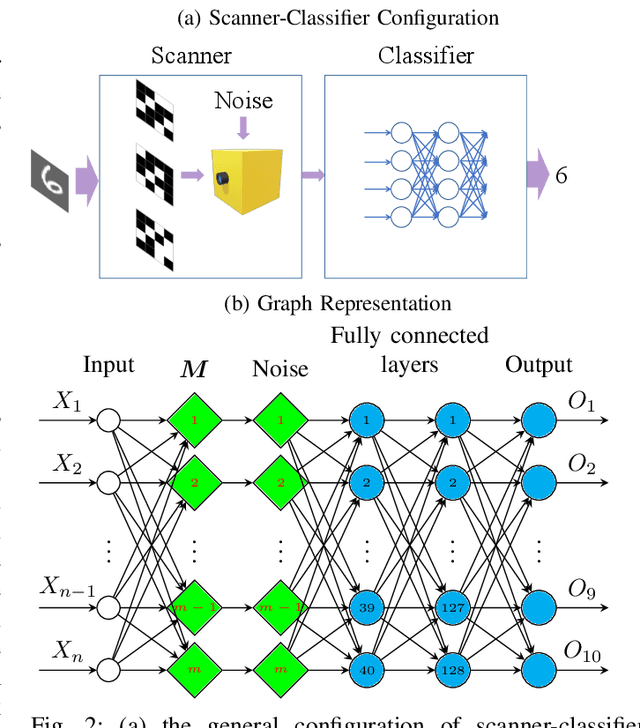
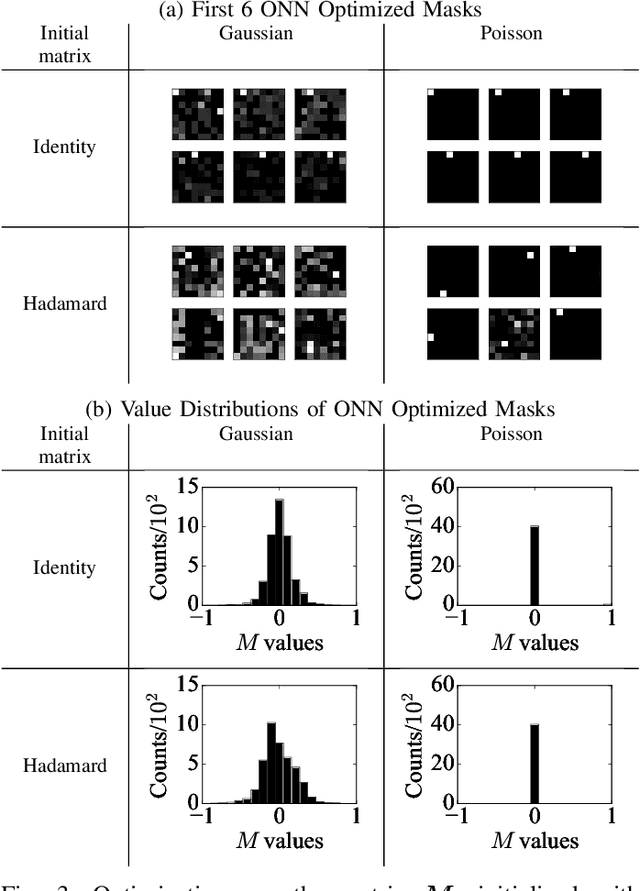
Optical coding has been widely adopted to improve the imaging techniques. Traditional coding strategies developed under additive Gaussian noise fail to perform optimally in the presence of Poisson noise. It has been observed in previous studies that coding performance varies significantly between these two noise models. In this work, we introduce a novel approach called selective sensing, which leverages training data to learn priors and optimizes the coding strategies for downstream classification tasks. By adapting to the specific characteristics of photon-counting sensors, the proposed method aims to improve coding performance under Poisson noise and enhance overall classification accuracy. Experimental and simulated results demonstrate the effectiveness of selective sensing in comparison to traditional coding strategies, highlighting its potential for practical applications in photon counting scenarios where Poisson noise are prevalent.

iToF2dToF: A Robust and Flexible Representation for Data-Driven Time-of-Flight Imaging

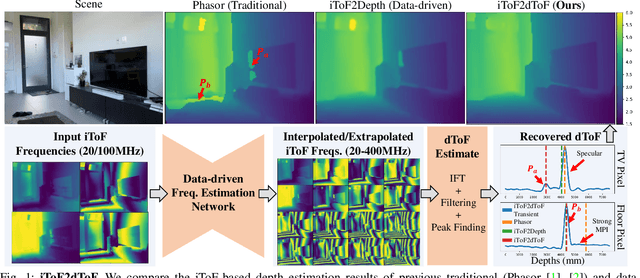
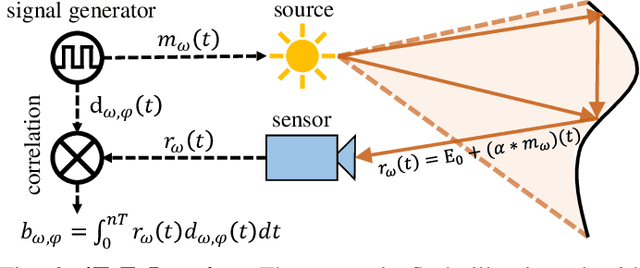
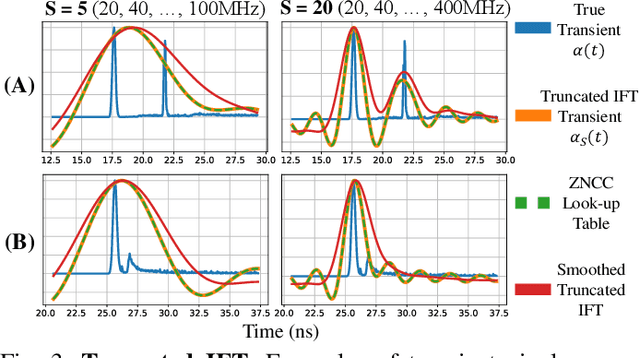
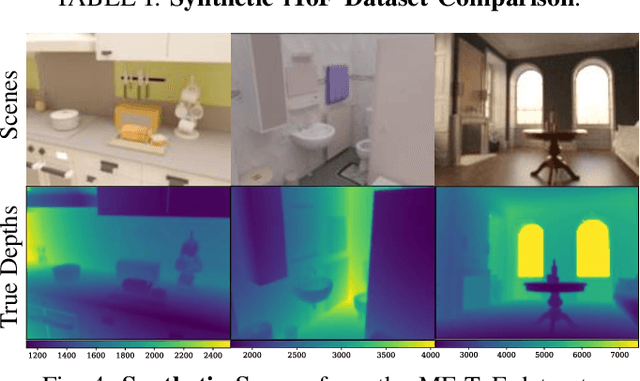
Indirect Time-of-Flight (iToF) cameras are a promising depth sensing technology. However, they are prone to errors caused by multi-path interference (MPI) and low signal-to-noise ratio (SNR). Traditional methods, after denoising, mitigate MPI by estimating a transient image that encodes depths. Recently, data-driven methods that jointly denoise and mitigate MPI have become state-of-the-art without using the intermediate transient representation. In this paper, we propose to revisit the transient representation. Using data-driven priors, we interpolate/extrapolate iToF frequencies and use them to estimate the transient image. Given direct ToF (dToF) sensors capture transient images, we name our method iToF2dToF. The transient representation is flexible. It can be integrated with different rule-based depth sensing algorithms that are robust to low SNR and can deal with ambiguous scenarios that arise in practice (e.g., specular MPI, optical cross-talk). We demonstrate the benefits of iToF2dToF over previous methods in real depth sensing scenarios.

Accelerating Permutation Testing in Voxel-wise Analysis through Subspace Tracking: A new plugin for SnPM

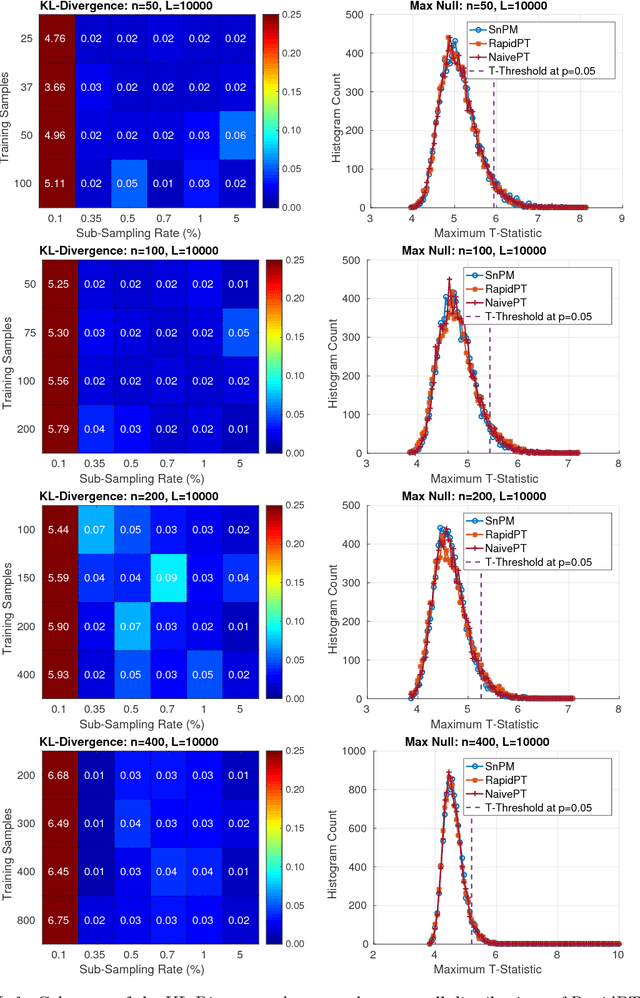
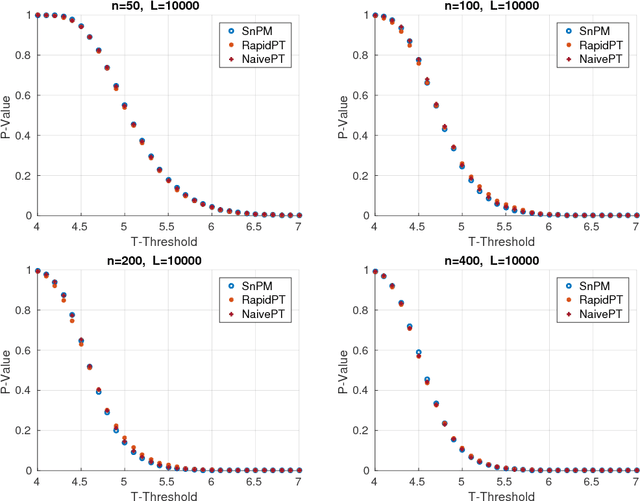
Permutation testing is a non-parametric method for obtaining the max null distribution used to compute corrected $p$-values that provide strong control of false positives. In neuroimaging, however, the computational burden of running such an algorithm can be significant. We find that by viewing the permutation testing procedure as the construction of a very large permutation testing matrix, $T$, one can exploit structural properties derived from the data and the test statistics to reduce the runtime under certain conditions. In particular, we see that $T$ is low-rank plus a low-variance residual. This makes $T$ a good candidate for low-rank matrix completion, where only a very small number of entries of $T$ ($\sim0.35\%$ of all entries in our experiments) have to be computed to obtain a good estimate. Based on this observation, we present RapidPT, an algorithm that efficiently recovers the max null distribution commonly obtained through regular permutation testing in voxel-wise analysis. We present an extensive validation on a synthetic dataset and four varying sized datasets against two baselines: Statistical NonParametric Mapping (SnPM13) and a standard permutation testing implementation (referred as NaivePT). We find that RapidPT achieves its best runtime performance on medium sized datasets ($50 \leq n \leq 200$), with speedups of 1.5x - 38x (vs. SnPM13) and 20x-1000x (vs. NaivePT). For larger datasets ($n \geq 200$) RapidPT outperforms NaivePT (6x - 200x) on all datasets, and provides large speedups over SnPM13 when more than 10000 permutations (2x - 15x) are needed. The implementation is a standalone toolbox and also integrated within SnPM13, able to leverage multi-core architectures when available.