Mitigating analytical variability in fMRI results with style transfer

We propose a novel approach to improve the reproducibility of neuroimaging results by converting statistic maps across different functional MRI pipelines. We make the assumption that pipelines can be considered as a style component of data and propose to use different generative models, among which, Diffusion Models (DM) to convert data between pipelines. We design a new DM-based unsupervised multi-domain image-to-image transition framework and constrain the generation of 3D fMRI statistic maps using the latent space of an auxiliary classifier that distinguishes statistic maps from different pipelines. We extend traditional sampling techniques used in DM to improve the transition performance. Our experiments demonstrate that our proposed methods are successful: pipelines can indeed be transferred, providing an important source of data augmentation for future medical studies.

Uncovering communities of pipelines in the task-fMRI analytical space

Functional magnetic resonance imaging analytical workflows are highly flexible with no definite consensus on how to choose a pipeline. While methods have been developed to explore this analytical space, there is still a lack of understanding of the relationships between the different pipelines. We use community detection algorithms to explore the pipeline space and assess its stability across different contexts. We show that there are subsets of pipelines that give similar results, especially those sharing specific parameters (e.g. number of motion regressors, software packages, etc.), with relative stability across groups of participants. By visualizing the differences between these subsets, we describe the effect of pipeline parameters and derive general relationships in the analytical space.

On the benefits of self-taught learning for brain decoding

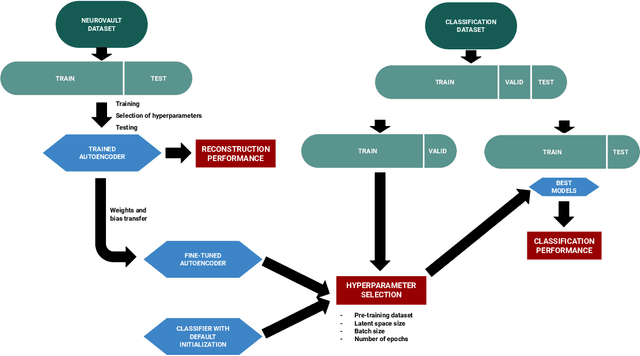
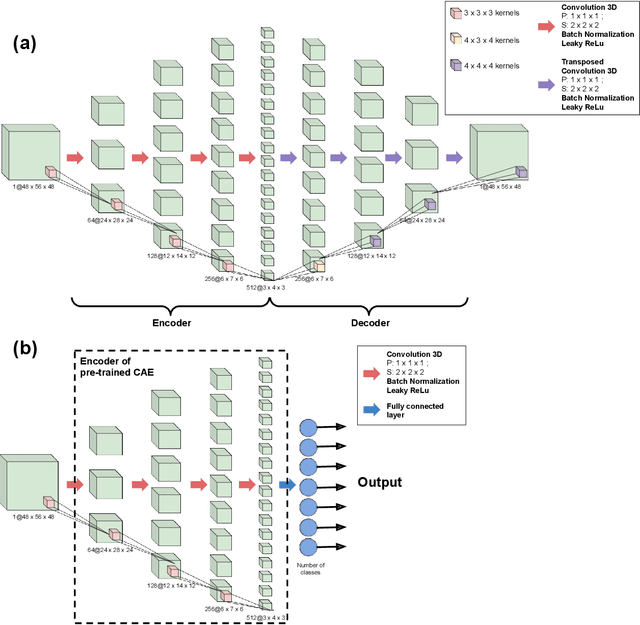
We study the benefits of using a large public neuroimaging database composed of fMRI statistic maps, in a self-taught learning framework, for improving brain decoding on new tasks. First, we leverage the NeuroVault database to train, on a selection of relevant statistic maps, a convolutional autoencoder to reconstruct these maps. Then, we use this trained encoder to initialize a supervised convolutional neural network to classify tasks or cognitive processes of unseen statistic maps from large collections of the NeuroVault database. We show that such a self-taught learning process always improves the performance of the classifiers but the magnitude of the benefits strongly depends on the number of data available both for pre-training and finetuning the models and on the complexity of the targeted downstream task.

Accelerating Permutation Testing in Voxel-wise Analysis through Subspace Tracking: A new plugin for SnPM

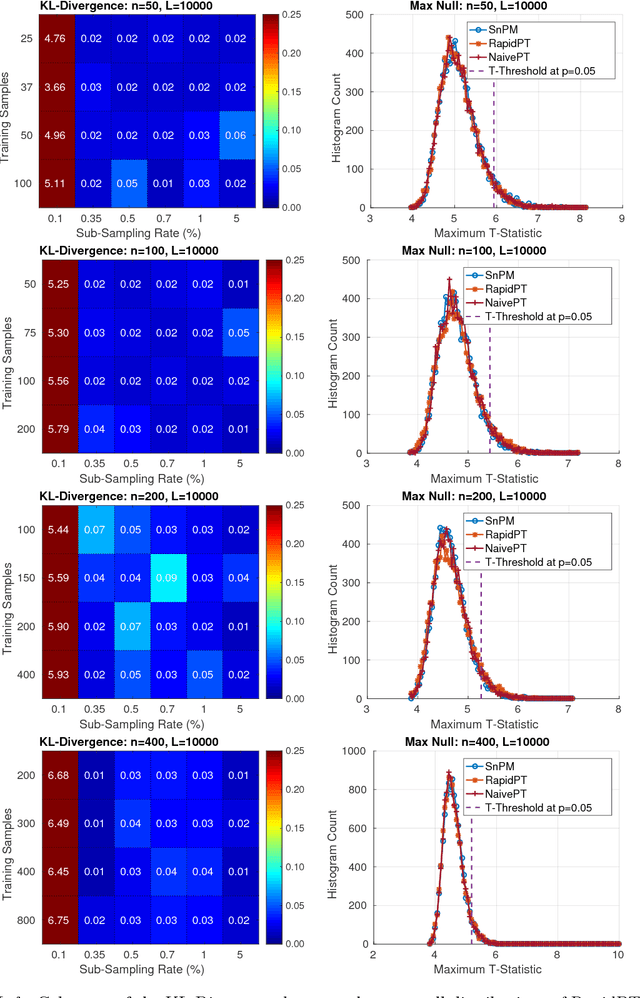
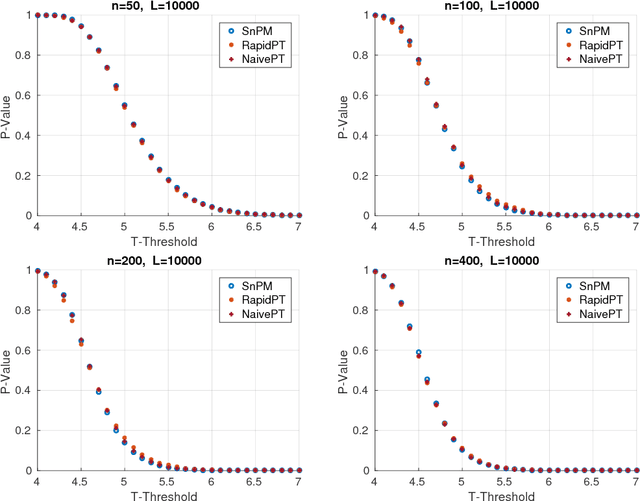
Permutation testing is a non-parametric method for obtaining the max null distribution used to compute corrected $p$-values that provide strong control of false positives. In neuroimaging, however, the computational burden of running such an algorithm can be significant. We find that by viewing the permutation testing procedure as the construction of a very large permutation testing matrix, $T$, one can exploit structural properties derived from the data and the test statistics to reduce the runtime under certain conditions. In particular, we see that $T$ is low-rank plus a low-variance residual. This makes $T$ a good candidate for low-rank matrix completion, where only a very small number of entries of $T$ ($\sim0.35\%$ of all entries in our experiments) have to be computed to obtain a good estimate. Based on this observation, we present RapidPT, an algorithm that efficiently recovers the max null distribution commonly obtained through regular permutation testing in voxel-wise analysis. We present an extensive validation on a synthetic dataset and four varying sized datasets against two baselines: Statistical NonParametric Mapping (SnPM13) and a standard permutation testing implementation (referred as NaivePT). We find that RapidPT achieves its best runtime performance on medium sized datasets ($50 \leq n \leq 200$), with speedups of 1.5x - 38x (vs. SnPM13) and 20x-1000x (vs. NaivePT). For larger datasets ($n \geq 200$) RapidPT outperforms NaivePT (6x - 200x) on all datasets, and provides large speedups over SnPM13 when more than 10000 permutations (2x - 15x) are needed. The implementation is a standalone toolbox and also integrated within SnPM13, able to leverage multi-core architectures when available.