The Perfect Blend: Redefining RLHF with Mixture of Judges

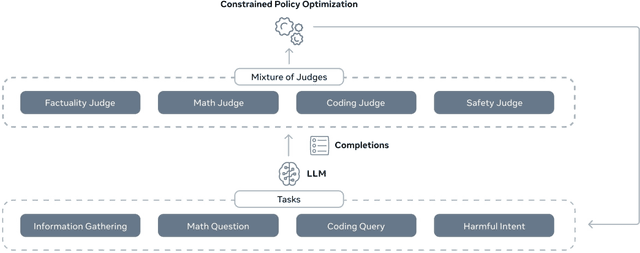
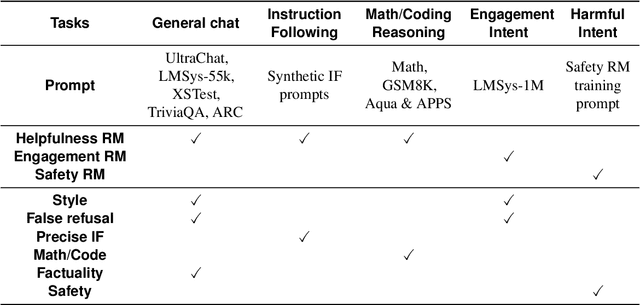
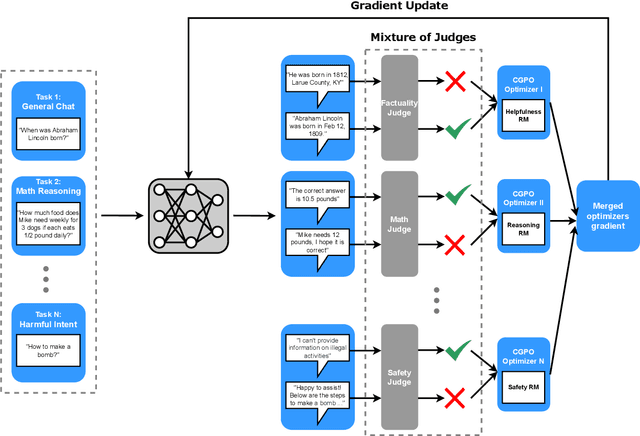
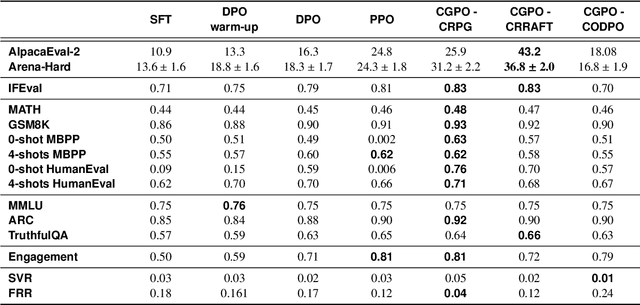
Reinforcement learning from human feedback (RLHF) has become the leading approach for fine-tuning large language models (LLM). However, RLHF has limitations in multi-task learning (MTL) due to challenges of reward hacking and extreme multi-objective optimization (i.e., trade-off of multiple and/or sometimes conflicting objectives). Applying RLHF for MTL currently requires careful tuning of the weights for reward model and data combinations. This is often done via human intuition and does not generalize. In this work, we introduce a novel post-training paradigm which we called Constrained Generative Policy Optimization (CGPO). The core of CGPO is Mixture of Judges (MoJ) with cost-efficient constrained policy optimization with stratification, which can identify the perfect blend in RLHF in a principled manner. It shows strong empirical results with theoretical guarantees, does not require extensive hyper-parameter tuning, and is plug-and-play in common post-training pipelines. Together, this can detect and mitigate reward hacking behaviors while reaching a pareto-optimal point across an extremely large number of objectives. Our empirical evaluations demonstrate that CGPO significantly outperforms standard RLHF algorithms like PPO and DPO across various tasks including general chat, STEM questions, instruction following, and coding. Specifically, CGPO shows improvements of 7.4% in AlpacaEval-2 (general chat), 12.5% in Arena-Hard (STEM & reasoning), and consistent gains in other domains like math and coding. Notably, PPO, while commonly used, is prone to severe reward hacking in popular coding benchmarks, which CGPO successfully addresses. This breakthrough in RLHF not only tackles reward hacking and extreme multi-objective optimization challenges but also advances the state-of-the-art in aligning general-purpose LLMs for diverse applications.

Adversarial Attacks on Gaussian Process Bandits

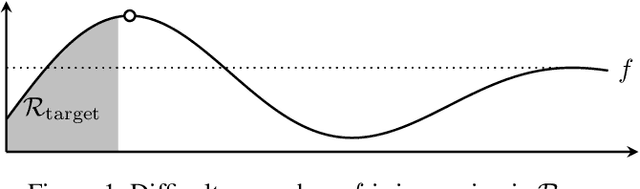
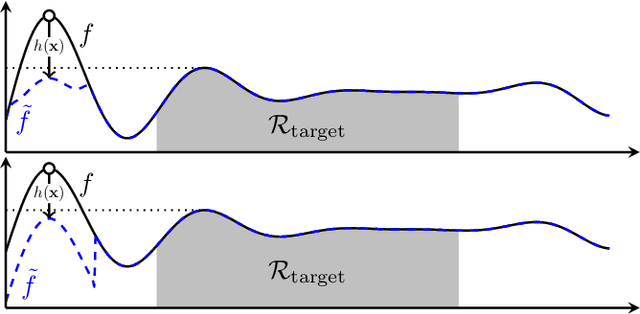
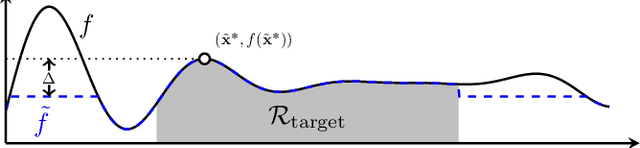
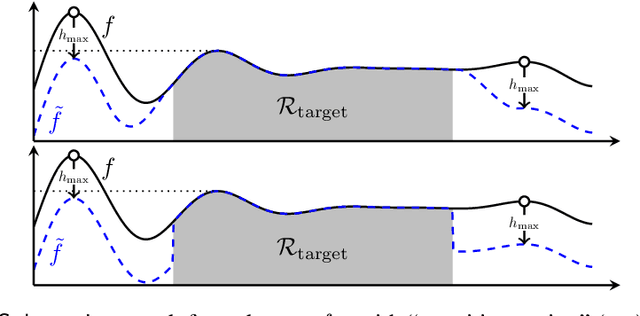
Gaussian processes (GP) are a widely-adopted tool used to sequentially optimize black-box functions, where evaluations are costly and potentially noisy. Recent works on GP bandits have proposed to move beyond random noise and devise algorithms robust to adversarial attacks. In this paper, we study this problem from the attacker's perspective, proposing various adversarial attack methods with differing assumptions on the attacker's strength and prior information. Our goal is to understand adversarial attacks on GP bandits from both a theoretical and practical perspective. We focus primarily on targeted attacks on the popular GP-UCB algorithm and a related elimination-based algorithm, based on adversarially perturbing the function $f$ to produce another function $\tilde{f}$ whose optima are in some region $\mathcal{R}_{\rm target}$. Based on our theoretical analysis, we devise both white-box attacks (known $f$) and black-box attacks (unknown $f$), with the former including a Subtraction attack and Clipping attack, and the latter including an Aggressive subtraction attack. We demonstrate that adversarial attacks on GP bandits can succeed in forcing the algorithm towards $\mathcal{R}_{\rm target}$ even with a low attack budget, and we compare our attacks' performance and efficiency on several real and synthetic functions.

High-Dimensional Bayesian Optimization via Tree-Structured Additive Models

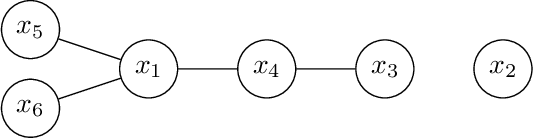
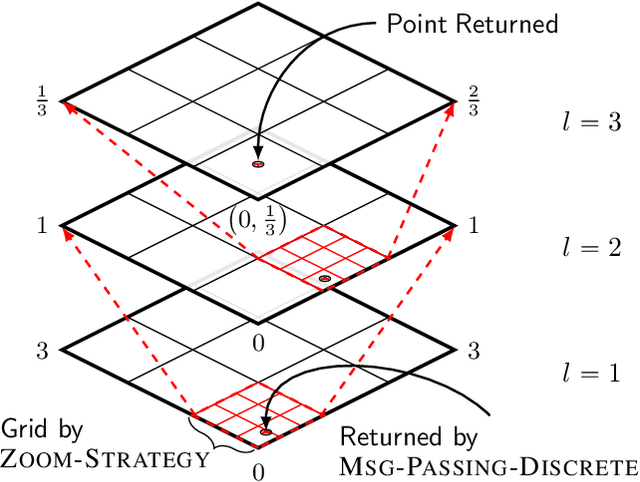
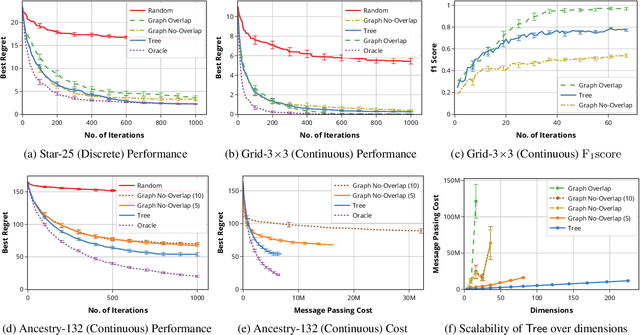
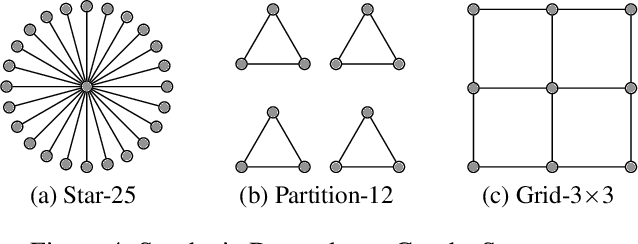
Bayesian Optimization (BO) has shown significant success in tackling expensive low-dimensional black-box optimization problems. Many optimization problems of interest are high-dimensional, and scaling BO to such settings remains an important challenge. In this paper, we consider generalized additive models in which low-dimensional functions with overlapping subsets of variables are composed to model a high-dimensional target function. Our goal is to lower the computational resources required and facilitate faster model learning by reducing the model complexity while retaining the sample-efficiency of existing methods. Specifically, we constrain the underlying dependency graphs to tree structures in order to facilitate both the structure learning and optimization of the acquisition function. For the former, we propose a hybrid graph learning algorithm based on Gibbs sampling and mutation. In addition, we propose a novel zooming-based algorithm that permits generalized additive models to be employed more efficiently in the case of continuous domains. We demonstrate and discuss the efficacy of our approach via a range of experiments on synthetic functions and real-world datasets.