Adversarial Attacks on Gaussian Process Bandits
Paper and Code
Oct 16, 2021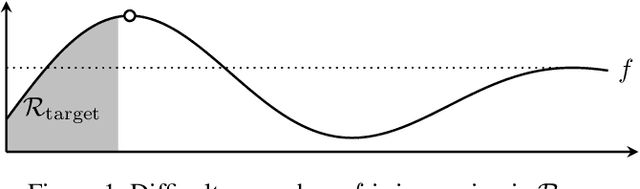
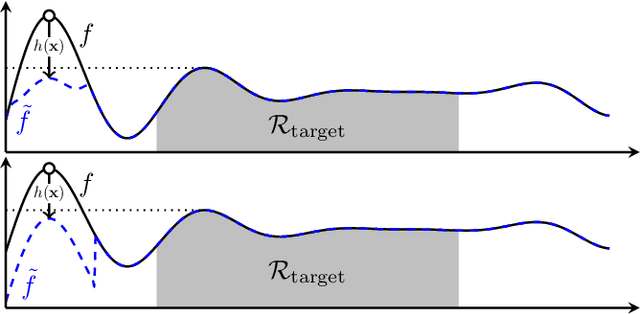
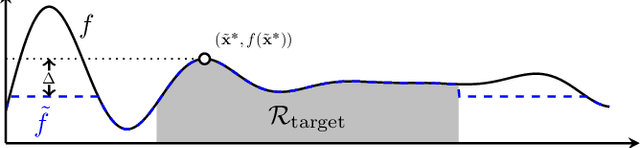
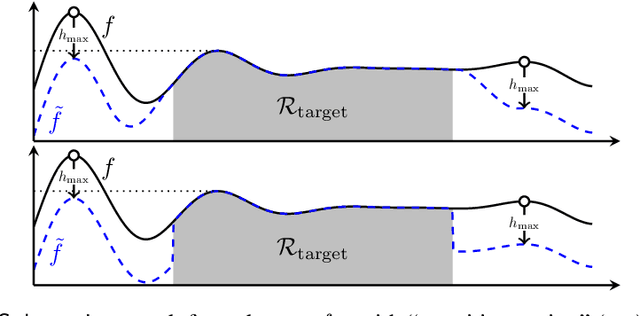
Gaussian processes (GP) are a widely-adopted tool used to sequentially optimize black-box functions, where evaluations are costly and potentially noisy. Recent works on GP bandits have proposed to move beyond random noise and devise algorithms robust to adversarial attacks. In this paper, we study this problem from the attacker's perspective, proposing various adversarial attack methods with differing assumptions on the attacker's strength and prior information. Our goal is to understand adversarial attacks on GP bandits from both a theoretical and practical perspective. We focus primarily on targeted attacks on the popular GP-UCB algorithm and a related elimination-based algorithm, based on adversarially perturbing the function $f$ to produce another function $\tilde{f}$ whose optima are in some region $\mathcal{R}_{\rm target}$. Based on our theoretical analysis, we devise both white-box attacks (known $f$) and black-box attacks (unknown $f$), with the former including a Subtraction attack and Clipping attack, and the latter including an Aggressive subtraction attack. We demonstrate that adversarial attacks on GP bandits can succeed in forcing the algorithm towards $\mathcal{R}_{\rm target}$ even with a low attack budget, and we compare our attacks' performance and efficiency on several real and synthetic functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge