High-Dimensional Bayesian Optimization via Tree-Structured Additive Models
Paper and Code
Dec 24, 2020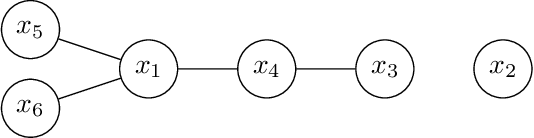
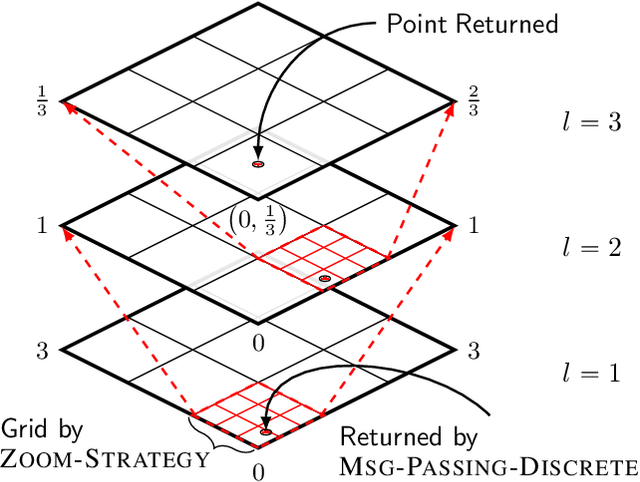
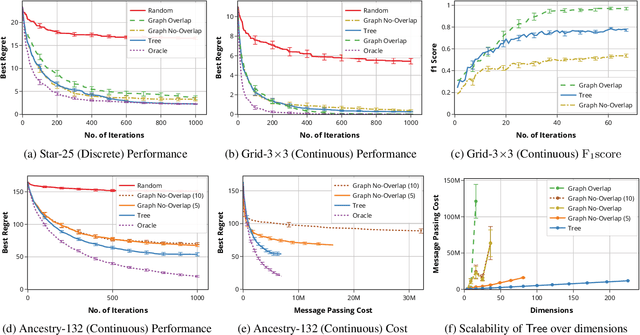
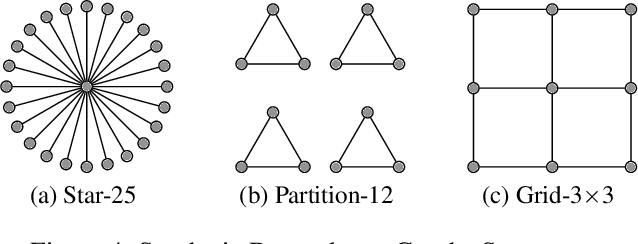
Bayesian Optimization (BO) has shown significant success in tackling expensive low-dimensional black-box optimization problems. Many optimization problems of interest are high-dimensional, and scaling BO to such settings remains an important challenge. In this paper, we consider generalized additive models in which low-dimensional functions with overlapping subsets of variables are composed to model a high-dimensional target function. Our goal is to lower the computational resources required and facilitate faster model learning by reducing the model complexity while retaining the sample-efficiency of existing methods. Specifically, we constrain the underlying dependency graphs to tree structures in order to facilitate both the structure learning and optimization of the acquisition function. For the former, we propose a hybrid graph learning algorithm based on Gibbs sampling and mutation. In addition, we propose a novel zooming-based algorithm that permits generalized additive models to be employed more efficiently in the case of continuous domains. We demonstrate and discuss the efficacy of our approach via a range of experiments on synthetic functions and real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge