How To Discover Short, Shorter, and the Shortest Proofs of Unsatisfiability: A Branch-and-Bound Approach for Resolution Proof Length Minimization

Modern software for propositional satisfiability problems gives a powerful automated reasoning toolkit, capable of outputting not only a satisfiable/unsatisfiable signal but also a justification of unsatisfiability in the form of resolution proof (or a more expressive proof), which is commonly used for verification purposes. Empirically, modern SAT solvers produce relatively short proofs, however, there are no inherent guarantees that these proofs cannot be significantly reduced. This paper proposes a novel branch-and-bound algorithm for finding the shortest resolution proofs; to this end, we introduce a layer list representation of proofs that groups clauses by their level of indirection. As we show, this representation breaks all permutational symmetries, thereby improving upon the state-of-the-art symmetry-breaking and informing the design of a novel workflow for proof minimization. In addition to that, we design pruning procedures that reason on proof length lower bound, clause subsumption, and dominance. Our experiments suggest that the proofs from state-of-the-art solvers could be shortened by 30-60% on the instances from SAT Competition 2002 and by 25-50% on small synthetic formulas. When treated as an algorithm for finding the shortest proof, our approach solves twice as many instances as the previous work based on SAT solving and reduces the time to optimality by orders of magnitude for the instances solved by both approaches.

In Search of Trees: Decision-Tree Policy Synthesis for Black-Box Systems via Search

Decision trees, owing to their interpretability, are attractive as control policies for (dynamical) systems. Unfortunately, constructing, or synthesising, such policies is a challenging task. Previous approaches do so by imitating a neural-network policy, approximating a tabular policy obtained via formal synthesis, employing reinforcement learning, or modelling the problem as a mixed-integer linear program. However, these works may require access to a hard-to-obtain accurate policy or a formal model of the environment (within reach of formal synthesis), and may not provide guarantees on the quality or size of the final tree policy. In contrast, we present an approach to synthesise optimal decision-tree policies given a black-box environment and specification, and a discretisation of the tree predicates, where optimality is defined with respect to the number of steps to achieve the goal. Our approach is a specialised search algorithm which systematically explores the (exponentially large) space of decision trees under the given discretisation. The key component is a novel pruning mechanism that significantly reduces the search space. Our approach represents a conceptually novel way of synthesising small decision-tree policies with optimality guarantees even for black-box environments with black-box specifications.

Optimal Survival Trees: A Dynamic Programming Approach

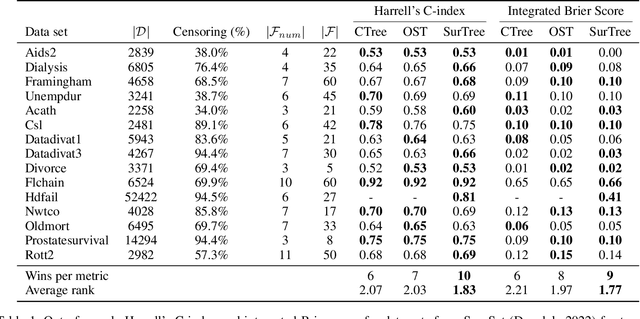
Survival analysis studies and predicts the time of death, or other singular unrepeated events, based on historical data, while the true time of death for some instances is unknown. Survival trees enable the discovery of complex nonlinear relations in a compact human comprehensible model, by recursively splitting the population and predicting a distinct survival distribution in each leaf node. We use dynamic programming to provide the first survival tree method with optimality guarantees, enabling the assessment of the optimality gap of heuristics. We improve the scalability of our method through a special algorithm for computing trees up to depth two. The experiments show that our method's run time even outperforms some heuristics for realistic cases while obtaining similar out-of-sample performance with the state-of-the-art.

Optimal Decision Trees for Separable Objectives: Pushing the Limits of Dynamic Programming

Global optimization of decision trees has shown to be promising in terms of accuracy, size, and consequently human comprehensibility. However, many of the methods used rely on general-purpose solvers for which scalability remains an issue. Dynamic programming methods have been shown to scale much better because they exploit the tree structure by solving subtrees as independent subproblems. However, this only works when an objective can be optimized separately for subtrees. We explore this relationship in detail and show necessary and sufficient conditions for such separability and generalize previous dynamic programming approaches into a framework that can optimize any combination of separable objectives and constraints. Experiments on four application domains show the general applicability of this framework, while outperforming the scalability of general-purpose solvers by a large margin.

Optimal Decision Trees for Nonlinear Metrics

Nonlinear metrics, such as the F1-score, Matthews correlation coefficient, and Fowlkes-Mallows index, are often used to evaluate the performance of machine learning models, in particular, when facing imbalanced datasets that contain more samples of one class than the other. Recent optimal decision tree algorithms have shown remarkable progress in producing trees that are optimal with respect to linear criteria, such as accuracy, but unfortunately nonlinear metrics remain a challenge. To address this gap, we propose a novel algorithm based on bi-objective optimisation, which treats misclassifications of each binary class as a separate objective. We show that, for a large class of metrics, the optimal tree lies on the Pareto frontier. Consequently, we obtain the optimal tree by using our method to generate the set of all nondominated trees. To the best of our knowledge, this is the first method to compute provably optimal decision trees for nonlinear metrics. Our approach leads to a trade-off when compared to optimising linear metrics: the resulting trees may be more desirable according to the given nonlinear metric at the expense of higher runtimes. Nevertheless, the experiments illustrate that runtimes are reasonable for majority of the tested datasets.

MurTree: Optimal Classification Trees via Dynamic Programming and Search

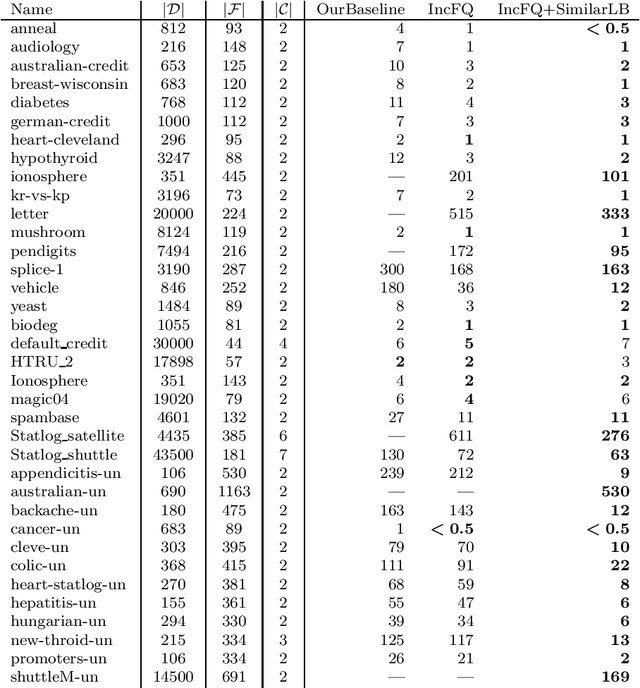
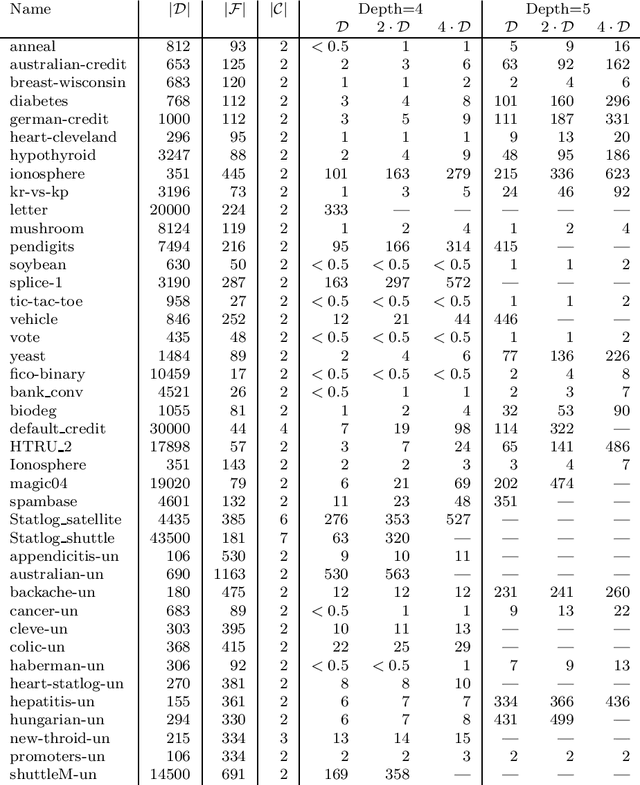
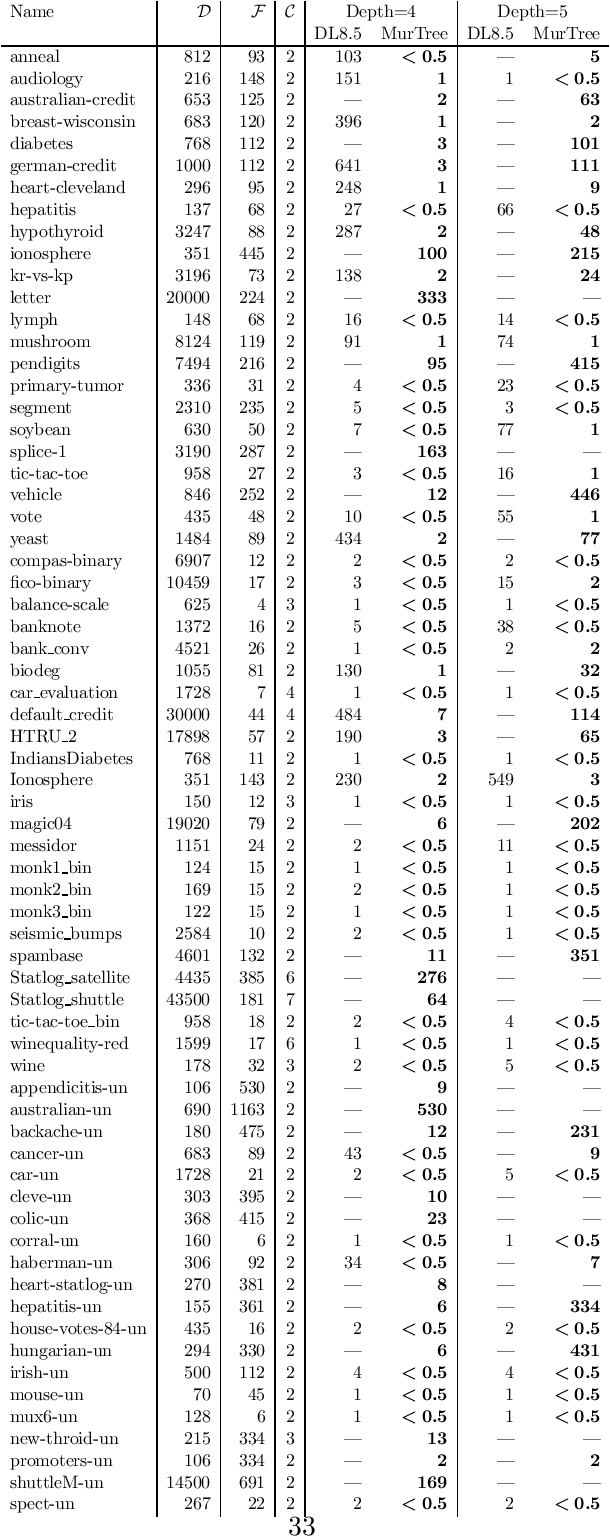
Decision tree learning is a widely used approach in machine learning, favoured in applications that require concise and interpretable models. Heuristic methods are traditionally used to quickly produce models with reasonably high accuracy. A commonly criticised point, however, is that the resulting trees may not necessarily be the best representation of the data in terms of accuracy, size, and other considerations such as fairness. In recent years, this motivated the development of optimal classification tree algorithms that globally optimise the decision tree in contrast to heuristic methods that perform a sequence of locally optimal decisions. We follow this line of work and provide a novel algorithm for learning optimal classification trees based on dynamic programming and search. Our algorithm supports constraints on the depth of the tree and number of nodes and we argue it can be extended with other requirements. The success of our approach is attributed to a series of specialised techniques that exploit properties unique to classification trees. Whereas algorithms for optimal classification trees have traditionally been plagued by high runtimes and limited scalability, we show in a detailed experimental study that our approach uses only a fraction of the time required by the state-of-the-art and can handle datasets with tens of thousands of instances, providing several orders of magnitude improvements and notably contributing towards the practical realisation of optimal decision trees.

Smart Predict-and-Optimize for Hard Combinatorial Optimization Problems

Combinatorial optimization assumes that all parameters of the optimization problem, e.g. the weights in the objective function is fixed. Often, these weights are mere estimates and increasingly machine learning techniques are used to for their estimation. Recently, Smart Predict and Optimize (SPO) has been proposed for problems with a linear objective function over the predictions, more specifically linear programming problems. It takes the regret of the predictions on the linear problem into account, by repeatedly solving it during learning. We investigate the use of SPO to solve more realistic discrete optimization problems. The main challenge is the repeated solving of the optimization problem. To this end, we investigate ways to relax the problem as well as warmstarting the learning and the solving. Our results show that even for discrete problems it often suffices to train by solving the relaxation in the SPO loss. Furthermore, this approach outperforms, for most instances, the state-of-the-art approach of Wilder, Dilkina, and Tambe. We experiment with weighted knapsack problems as well as complex scheduling problems and show for the first time that a predict-and-optimize approach can successfully be used on large-scale combinatorial optimization problems.