How To Discover Short, Shorter, and the Shortest Proofs of Unsatisfiability: A Branch-and-Bound Approach for Resolution Proof Length Minimization

Modern software for propositional satisfiability problems gives a powerful automated reasoning toolkit, capable of outputting not only a satisfiable/unsatisfiable signal but also a justification of unsatisfiability in the form of resolution proof (or a more expressive proof), which is commonly used for verification purposes. Empirically, modern SAT solvers produce relatively short proofs, however, there are no inherent guarantees that these proofs cannot be significantly reduced. This paper proposes a novel branch-and-bound algorithm for finding the shortest resolution proofs; to this end, we introduce a layer list representation of proofs that groups clauses by their level of indirection. As we show, this representation breaks all permutational symmetries, thereby improving upon the state-of-the-art symmetry-breaking and informing the design of a novel workflow for proof minimization. In addition to that, we design pruning procedures that reason on proof length lower bound, clause subsumption, and dominance. Our experiments suggest that the proofs from state-of-the-art solvers could be shortened by 30-60% on the instances from SAT Competition 2002 and by 25-50% on small synthetic formulas. When treated as an algorithm for finding the shortest proof, our approach solves twice as many instances as the previous work based on SAT solving and reduces the time to optimality by orders of magnitude for the instances solved by both approaches.

A review of approaches to modeling applied vehicle routing problems

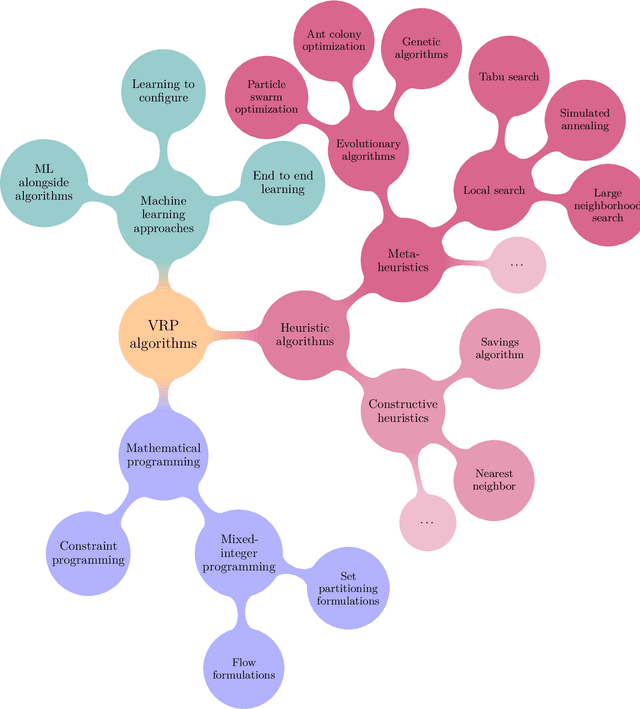
Due to the practical importance of vehicle routing problems (VRP), there exists an ever-growing body of research in algorithms and (meta)heuristics for solving such problems. However, the diversity of VRP domains creates the separate problem of modeling such problems -- describing the domain entities (and, in particular, the planning decisions), the set of valid planning decisions, and the preferences between different plans. In this paper, we review the approaches for modeling vehicle routing problems. To make the comparison more straightforward, we formulate several criteria for evaluating modeling methods reflecting the practical requirements of the development of optimization algorithms for such problems. Finally, as a result of this comparison, we discuss several future research avenues in the field of modeling VRP domains.