Optimal Invariant Bases for Atomistic Machine Learning

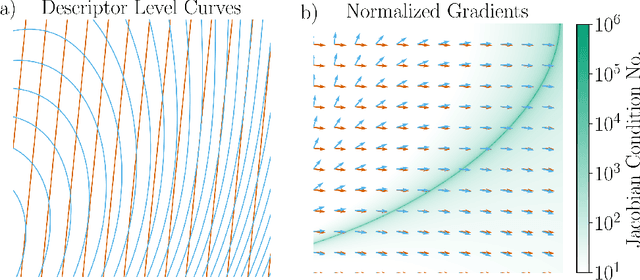
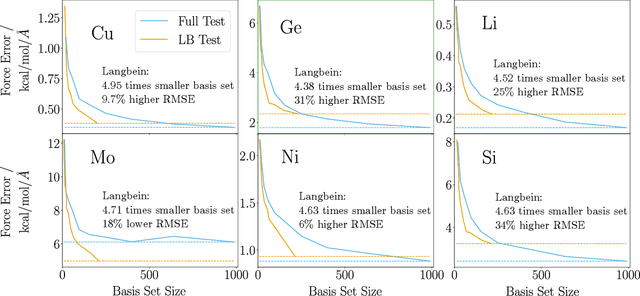
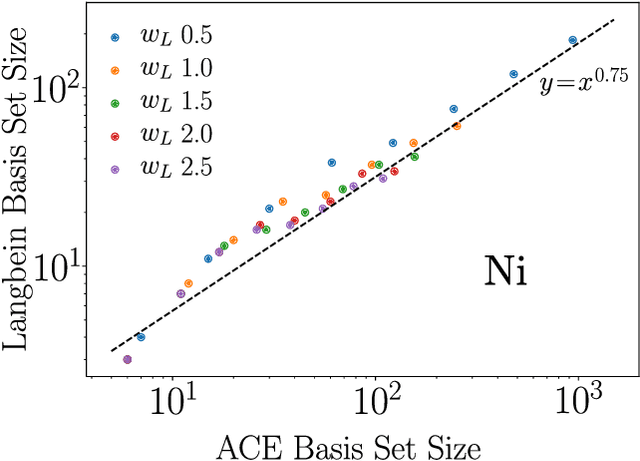
The representation of atomic configurations for machine learning models has led to the development of numerous descriptors, often to describe the local environment of atoms. However, many of these representations are incomplete and/or functionally dependent. Incomplete descriptor sets are unable to represent all meaningful changes in the atomic environment. Complete constructions of atomic environment descriptors, on the other hand, often suffer from a high degree of functional dependence, where some descriptors can be written as functions of the others. These redundant descriptors do not provide additional power to discriminate between different atomic environments and increase the computational burden. By employing techniques from the pattern recognition literature to existing atomistic representations, we remove descriptors that are functions of other descriptors to produce the smallest possible set that satisfies completeness. We apply this in two ways: first we refine an existing description, the Atomistic Cluster Expansion. We show that this yields a more efficient subset of descriptors. Second, we augment an incomplete construction based on a scalar neural network, yielding a new message-passing network architecture that can recognize up to 5-body patterns in each neuron by taking advantage of an optimal set of Cartesian tensor invariants. This architecture shows strong accuracy on state-of-the-art benchmarks while retaining low computational cost. Our results not only yield improved models, but point the way to classes of invariant bases that minimize cost while maximizing expressivity for a host of applications.

Flexible Moment-Invariant Bases from Irreducible Tensors

Moment invariants are a powerful tool for the generation of rotation-invariant descriptors needed for many applications in pattern detection, classification, and machine learning. A set of invariants is optimal if it is complete, independent, and robust against degeneracy in the input. In this paper, we show that the current state of the art for the generation of these bases of moment invariants, despite being robust against moment tensors being identically zero, is vulnerable to a degeneracy that is common in real-world applications, namely spherical functions. We show how to overcome this vulnerability by combining two popular moment invariant approaches: one based on spherical harmonics and one based on Cartesian tensor algebra.

Ensemble Knowledge Distillation for Machine Learning Interatomic Potentials

Machine learning interatomic potentials (MLIPs) are a promising tool to accelerate atomistic simulations and molecular property prediction. The quality of MLIPs strongly depends on the quantity of available training data as well as the quantum chemistry (QC) level of theory used to generate that data. Datasets generated with high-fidelity QC methods, such as coupled cluster, are typically restricted to small molecules and may be missing energy gradients. With this limited quantity of data, it is often difficult to train good MLIP models. We present an ensemble knowledge distillation (EKD) method to improve MLIP accuracy when trained to energy-only datasets. In our EKD approach, first, multiple teacher models are trained to QC energies and then used to generate atomic forces for all configurations in the dataset. Next, a student MLIP is trained to both QC energies and to ensemble-averaged forces generated by the teacher models. We apply this workflow on the ANI-1ccx dataset which consists of organic molecules with configuration energies computed at the coupled cluster level of theory. The resulting student MLIPs achieve new state-of-the-art accuracy on the out-of-sample COMP6 benchmark and improved stability for molecular dynamics simulations. The EKD approach for MLIP is broadly applicable for chemical, biomolecular and materials science simulations.

Teacher-student training improves accuracy and efficiency of machine learning inter-atomic potentials

Machine learning inter-atomic potentials (MLIPs) are revolutionizing the field of molecular dynamics (MD) simulations. Recent MLIPs have tended towards more complex architectures trained on larger datasets. The resulting increase in computational and memory costs may prohibit the application of these MLIPs to perform large-scale MD simulations. Here, we present a teacher-student training framework in which the latent knowledge from the teacher (atomic energies) is used to augment the students' training. We show that the light-weight student MLIPs have faster MD speeds at a fraction of the memory footprint compared to the teacher models. Remarkably, the student models can even surpass the accuracy of the teachers, even though both are trained on the same quantum chemistry dataset. Our work highlights a practical method for MLIPs to reduce the resources required for large-scale MD simulations.

Thermodynamic Transferability in Coarse-Grained Force Fields using Graph Neural Networks

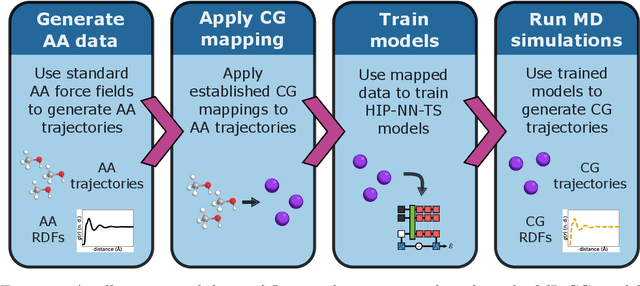
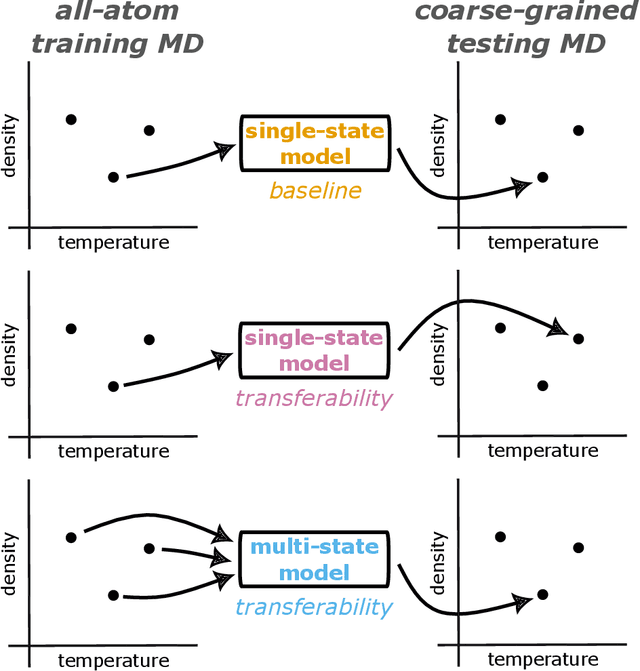
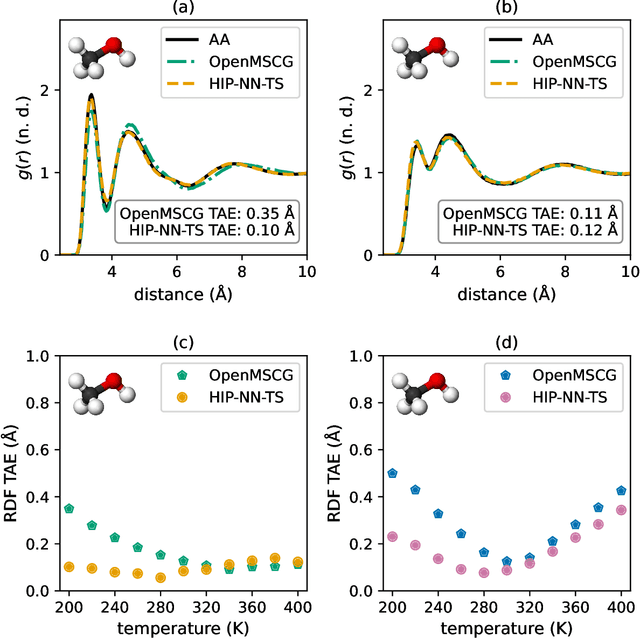
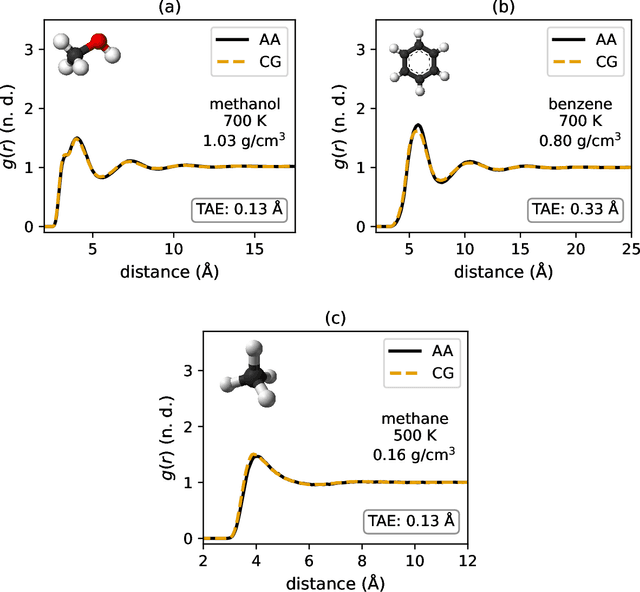
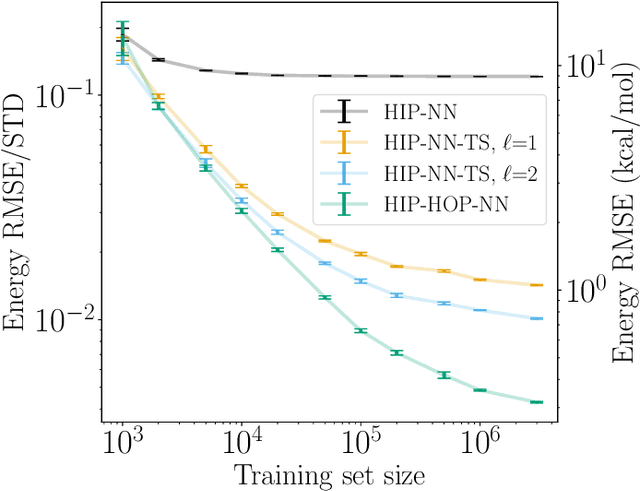
Coarse-graining is a molecular modeling technique in which an atomistic system is represented in a simplified fashion that retains the most significant system features that contribute to a target output, while removing the degrees of freedom that are less relevant. This reduction in model complexity allows coarse-grained molecular simulations to reach increased spatial and temporal scales compared to corresponding all-atom models. A core challenge in coarse-graining is to construct a force field that represents the interactions in the new representation in a way that preserves the atomistic-level properties. Many approaches to building coarse-grained force fields have limited transferability between different thermodynamic conditions as a result of averaging over internal fluctuations at a specific thermodynamic state point. Here, we use a graph-convolutional neural network architecture, the Hierarchically Interacting Particle Neural Network with Tensor Sensitivity (HIP-NN-TS), to develop a highly automated training pipeline for coarse grained force fields which allows for studying the transferability of coarse-grained models based on the force-matching approach. We show that this approach not only yields highly accurate force fields, but also that these force fields are more transferable through a variety of thermodynamic conditions. These results illustrate the potential of machine learning techniques such as graph neural networks to improve the construction of transferable coarse-grained force fields.