Optimal Invariant Bases for Atomistic Machine Learning

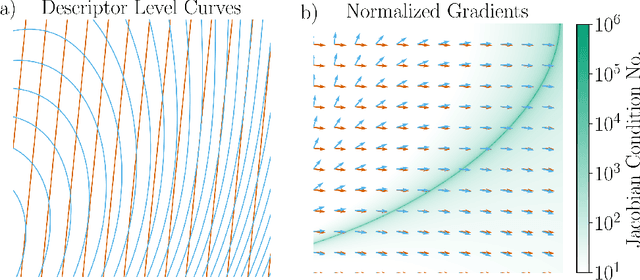
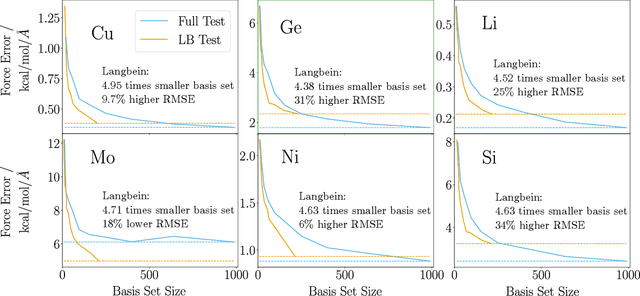
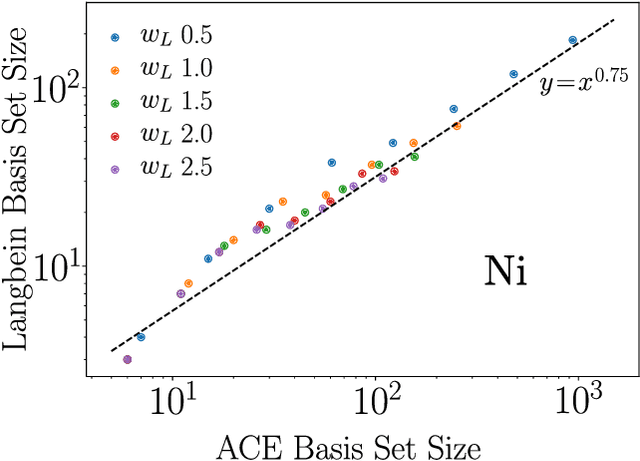
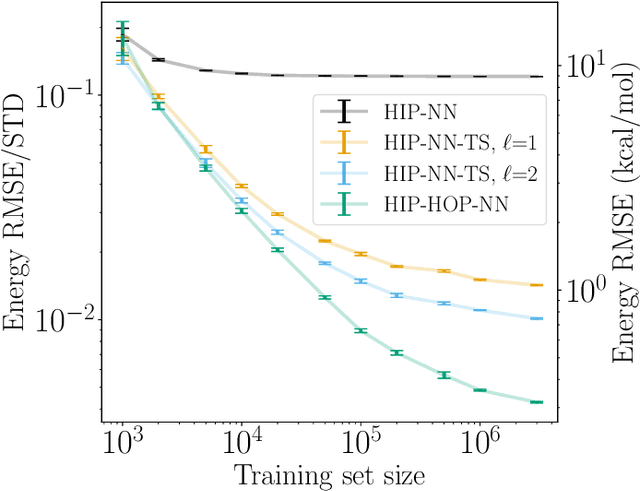
The representation of atomic configurations for machine learning models has led to the development of numerous descriptors, often to describe the local environment of atoms. However, many of these representations are incomplete and/or functionally dependent. Incomplete descriptor sets are unable to represent all meaningful changes in the atomic environment. Complete constructions of atomic environment descriptors, on the other hand, often suffer from a high degree of functional dependence, where some descriptors can be written as functions of the others. These redundant descriptors do not provide additional power to discriminate between different atomic environments and increase the computational burden. By employing techniques from the pattern recognition literature to existing atomistic representations, we remove descriptors that are functions of other descriptors to produce the smallest possible set that satisfies completeness. We apply this in two ways: first we refine an existing description, the Atomistic Cluster Expansion. We show that this yields a more efficient subset of descriptors. Second, we augment an incomplete construction based on a scalar neural network, yielding a new message-passing network architecture that can recognize up to 5-body patterns in each neuron by taking advantage of an optimal set of Cartesian tensor invariants. This architecture shows strong accuracy on state-of-the-art benchmarks while retaining low computational cost. Our results not only yield improved models, but point the way to classes of invariant bases that minimize cost while maximizing expressivity for a host of applications.

Constructing Effective Machine Learning Models for the Sciences: A Multidisciplinary Perspective

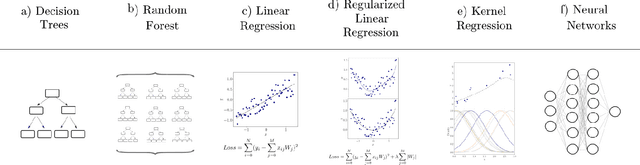
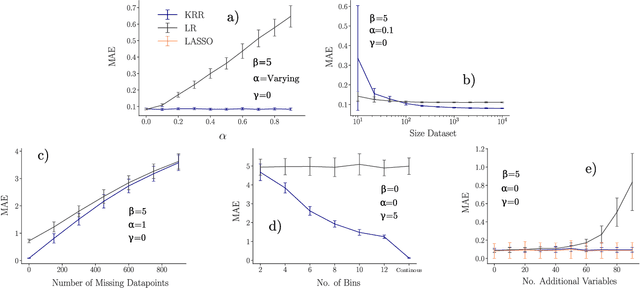
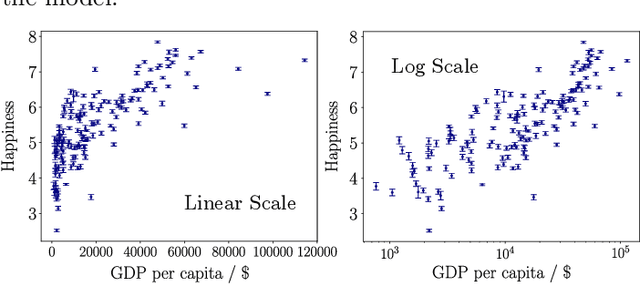
Learning from data has led to substantial advances in a multitude of disciplines, including text and multimedia search, speech recognition, and autonomous-vehicle navigation. Can machine learning enable similar leaps in the natural and social sciences? This is certainly the expectation in many scientific fields and recent years have seen a plethora of applications of non-linear models to a wide range of datasets. However, flexible non-linear solutions will not always improve upon manually adding transforms and interactions between variables to linear regression models. We discuss how to recognize this before constructing a data-driven model and how such analysis can help us move to intrinsically interpretable regression models. Furthermore, for a variety of applications in the natural and social sciences we demonstrate why improvements may be seen with more complex regression models and why they may not.