Optimal Invariant Bases for Atomistic Machine Learning

The representation of atomic configurations for machine learning models has led to the development of numerous descriptors, often to describe the local environment of atoms. However, many of these representations are incomplete and/or functionally dependent. Incomplete descriptor sets are unable to represent all meaningful changes in the atomic environment. Complete constructions of atomic environment descriptors, on the other hand, often suffer from a high degree of functional dependence, where some descriptors can be written as functions of the others. These redundant descriptors do not provide additional power to discriminate between different atomic environments and increase the computational burden. By employing techniques from the pattern recognition literature to existing atomistic representations, we remove descriptors that are functions of other descriptors to produce the smallest possible set that satisfies completeness. We apply this in two ways: first we refine an existing description, the Atomistic Cluster Expansion. We show that this yields a more efficient subset of descriptors. Second, we augment an incomplete construction based on a scalar neural network, yielding a new message-passing network architecture that can recognize up to 5-body patterns in each neuron by taking advantage of an optimal set of Cartesian tensor invariants. This architecture shows strong accuracy on state-of-the-art benchmarks while retaining low computational cost. Our results not only yield improved models, but point the way to classes of invariant bases that minimize cost while maximizing expressivity for a host of applications.

Flexible Moment-Invariant Bases from Irreducible Tensors

Moment invariants are a powerful tool for the generation of rotation-invariant descriptors needed for many applications in pattern detection, classification, and machine learning. A set of invariants is optimal if it is complete, independent, and robust against degeneracy in the input. In this paper, we show that the current state of the art for the generation of these bases of moment invariants, despite being robust against moment tensors being identically zero, is vulnerable to a degeneracy that is common in real-world applications, namely spherical functions. We show how to overcome this vulnerability by combining two popular moment invariant approaches: one based on spherical harmonics and one based on Cartesian tensor algebra.

Detection of Outer Rotations on 3D-Vector Fields with Iterative Geometric Correlation and its Efficiency

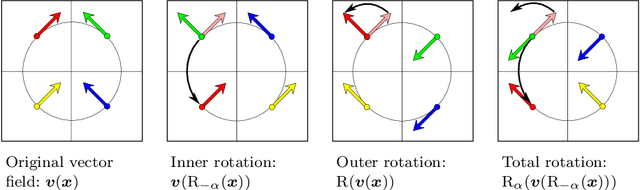
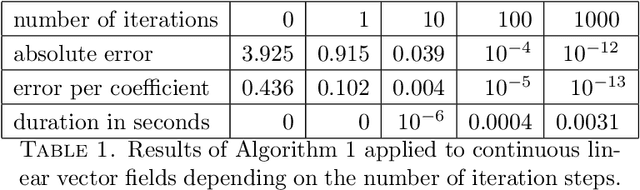
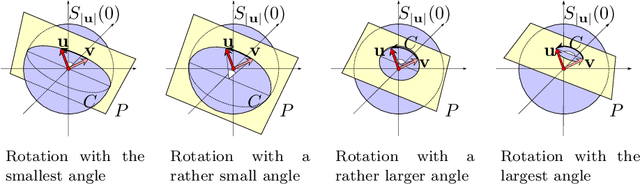
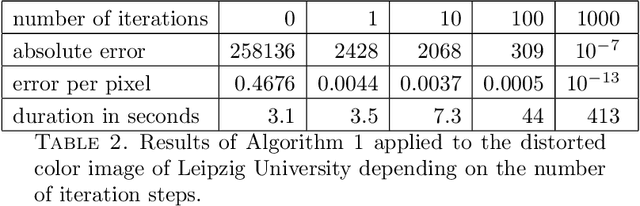
Correlation is a common technique for the detection of shifts. Its generalization to the multidimensional geometric correlation in Clifford algebras has been proven a useful tool for color image processing, because it additionally contains information about a rotational misalignment. But so far the exact correction of a three-dimensional outer rotation could only be achieved in certain special cases. In this paper we prove that applying the geometric correlation iteratively has the potential to detect the outer rotational misalignment for arbitrary three-dimensional vector fields. We further present the explicit iterative algorithm, analyze its efficiency detecting the rotational misalignment in the color space of a color image. The experiments suggest a method for the acceleration of the algorithm, which is practically tested with great success.