Detection of Outer Rotations on 3D-Vector Fields with Iterative Geometric Correlation and its Efficiency

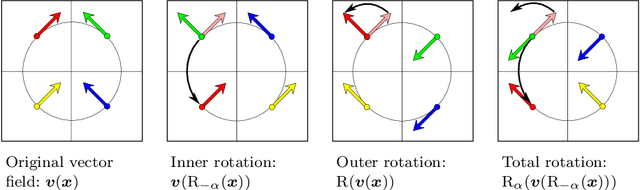
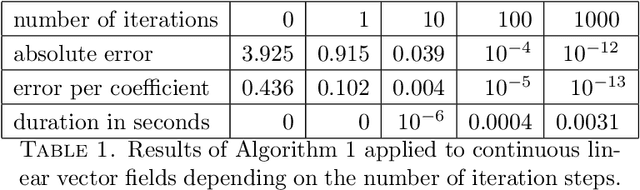
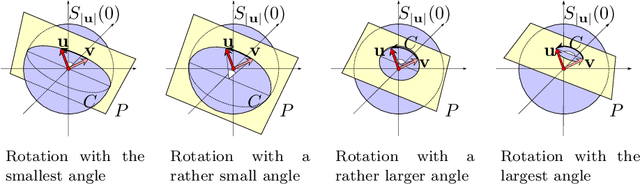
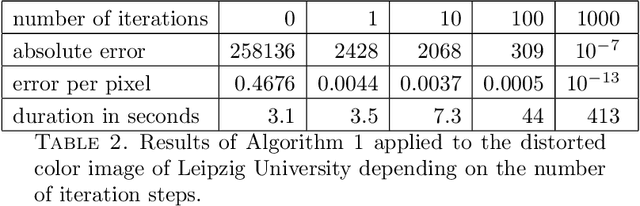
Correlation is a common technique for the detection of shifts. Its generalization to the multidimensional geometric correlation in Clifford algebras has been proven a useful tool for color image processing, because it additionally contains information about a rotational misalignment. But so far the exact correction of a three-dimensional outer rotation could only be achieved in certain special cases. In this paper we prove that applying the geometric correlation iteratively has the potential to detect the outer rotational misalignment for arbitrary three-dimensional vector fields. We further present the explicit iterative algorithm, analyze its efficiency detecting the rotational misalignment in the color space of a color image. The experiments suggest a method for the acceleration of the algorithm, which is practically tested with great success.

Clifford Fourier-Mellin transform with two real square roots of -1 in Cl(p,q), p+q=2

We describe a non-commutative generalization of the complex Fourier-Mellin transform to Clifford algebra valued signal functions over the domain $\R^{p,q}$ taking values in Cl(p,q), p+q=2. Keywords: algebra, Fourier transforms; Logic, set theory, and algebra, Fourier analysis, Integral transforms

Algebraic foundations of split hypercomplex nonlinear adaptive filtering

A split hypercomplex learning algorithm for the training of nonlinear finite impulse response adaptive filters for the processing of hypercomplex signals of any dimension is proposed. The derivation strictly takes into account the laws of hypercomplex algebra and hypercomplex calculus, some of which have been neglected in existing learning approaches (e.g. for quaternions). Already in the case of quaternions we can predict improvements in performance of hypercomplex processes. The convergence of the proposed algorithms is rigorously analyzed. Keywords: Quaternionic adaptive filtering, Hypercomplex adaptive filtering, Nonlinear adaptive filtering, Hypercomplex Multilayer Perceptron, Clifford geometric algebra

Quaternionic Fourier-Mellin Transform

In this contribution we generalize the classical Fourier Mellin transform [S. Dorrode and F. Ghorbel, Robust and efficient Fourier-Mellin transform approximations for gray-level image reconstruction and complete invariant description, Computer Vision and Image Understanding, 83(1) (2001), 57-78, DOI 10.1006/cviu.2001.0922.], which transforms functions $f$ representing, e.g., a gray level image defined over a compact set of $\mathbb{R}^2$. The quaternionic Fourier Mellin transform (QFMT) applies to functions $f: \mathbb{R}^2 \rightarrow \mathbb{H}$, for which $|f|$ is summable over $\mathbb{R}_+^* \times \mathbb{S}^1$ under the measure $d\theta \frac{dr}{r}$. $\mathbb{R}_+^*$ is the multiplicative group of positive and non-zero real numbers. We investigate the properties of the QFMT similar to the investigation of the quaternionic Fourier Transform (QFT) in [E. Hitzer, Quaternion Fourier Transform on Quaternion Fields and Generalizations, Advances in Applied Clifford Algebras, 17(3) (2007), 497-517.; E. Hitzer, Directional Uncertainty Principle for Quaternion Fourier Transforms, Advances in Applied Clifford Algebras, 20(2) (2010), 271-284, online since 08 July 2009.].

Non-constant bounded holomorphic functions of hyperbolic numbers - Candidates for hyperbolic activation functions

The Liouville theorem states that bounded holomorphic complex functions are necessarily constant. Holomorphic functions fulfill the socalled Cauchy-Riemann (CR) conditions. The CR conditions mean that a complex $z$-derivative is independent of the direction. Holomorphic functions are ideal for activation functions of complex neural networks, but the Liouville theorem makes them useless. Yet recently the use of hyperbolic numbers, lead to the construction of hyperbolic number neural networks. We will describe the Cauchy-Riemann conditions for hyperbolic numbers and show that there exists a new interesting type of bounded holomorphic functions of hyperbolic numbers, which are not constant. We give examples of such functions. They therefore substantially expand the available candidates for holomorphic activation functions for hyperbolic number neural networks. Keywords: Hyperbolic numbers, Liouville theorem, Cauchy-Riemann conditions, bounded holomorphic functions

OPS-QFTs: A new type of quaternion Fourier transforms based on the orthogonal planes split with one or two general pure quaternions

We explain the orthogonal planes split (OPS) of quaternions based on the arbitrary choice of one or two linearly independent pure unit quaternions $f,g$. Next we systematically generalize the quaternionic Fourier transform (QFT) applied to quaternion fields to conform with the OPS determined by $f,g$, or by only one pure unit quaternion $f$, comment on their geometric meaning, and establish inverse transformations. Keywords: Clifford geometric algebra, quaternion geometry, quaternion Fourier transform, inverse Fourier transform, orthogonal planes split

Geometric operations implemented by conformal geometric algebra neural nodes

Geometric algebra is an optimal frame work for calculating with vectors. The geometric algebra of a space includes elements that represent all the its subspaces (lines, planes, volumes, ...). Conformal geometric algebra expands this approach to elementary representations of arbitrary points, point pairs, lines, circles, planes and spheres. Apart from including curved objects, conformal geometric algebra has an elegant unified quaternion like representation for all proper and improper Euclidean transformations, including reflections at spheres, general screw transformations and scaling. Expanding the concepts of real and complex neurons we arrive at the new powerful concept of conformal geometric algebra neurons. These neurons can easily take the above mentioned geometric objects or sets of these objects as inputs and apply a wide range of geometric transformations via the geometric algebra valued weights.

Quaternion Fourier Transform on Quaternion Fields and Generalizations

We treat the quaternionic Fourier transform (QFT) applied to quaternion fields and investigate QFT properties useful for applications. Different forms of the QFT lead us to different Plancherel theorems. We relate the QFT computation for quaternion fields to the QFT of real signals. We research the general linear ($GL$) transformation behavior of the QFT with matrices, Clifford geometric algebra and with examples. We finally arrive at wide-ranging non-commutative multivector FT generalizations of the QFT. Examples given are new volume-time and spacetime algebra Fourier transformations.

Applications of Clifford's Geometric Algebra

We survey the development of Clifford's geometric algebra and some of its engineering applications during the last 15 years. Several recently developed applications and their merits are discussed in some detail. We thus hope to clearly demonstrate the benefit of developing problem solutions in a unified framework for algebra and geometry with the widest possible scope: from quantum computing and electromagnetism to satellite navigation, from neural computing to camera geometry, image processing, robotics and beyond.