Eduard Tulchinskii
Edge-wise Topological Divergence Gaps: Guiding Search in Combinatorial Optimization
Dec 16, 2025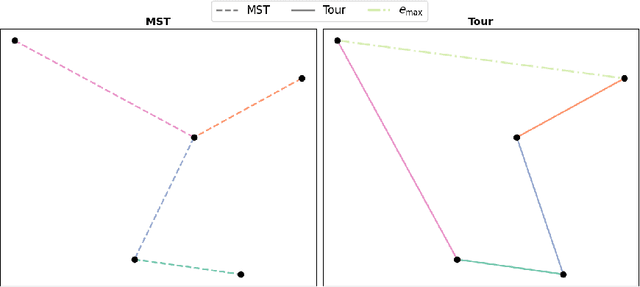
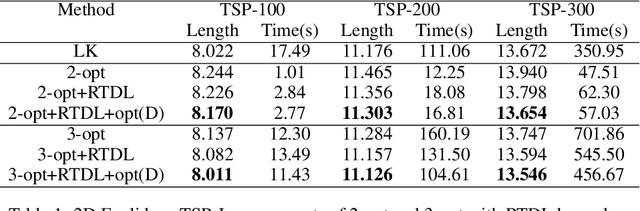
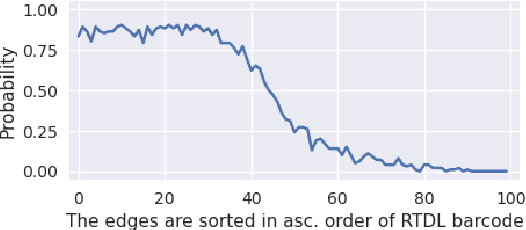
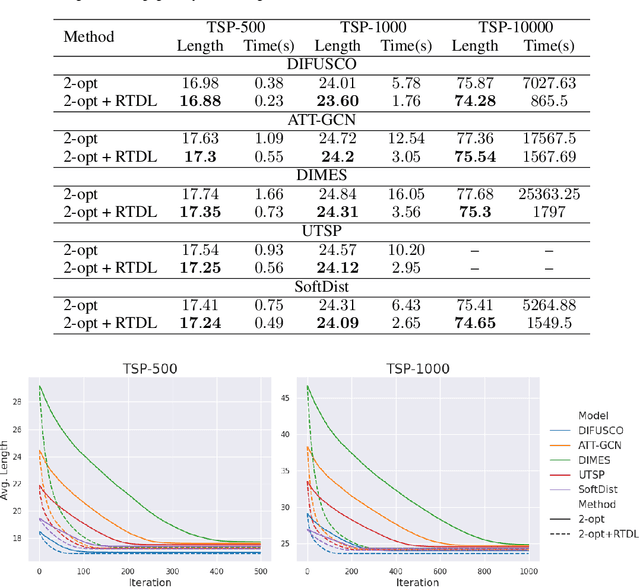
Abstract:We introduce a topological feedback mechanism for the Travelling Salesman Problem (TSP) by analyzing the divergence between a tour and the minimum spanning tree (MST). Our key contribution is a canonical decomposition theorem that expresses the tour-MST gap as edge-wise topology-divergence gaps from the RTD-Lite barcode. Based on this, we develop a topological guidance for 2-opt and 3-opt heuristics that increases their performance. We carry out experiments with fine-optimization of tours obtained from heatmap-based methods, TSPLIB, and random instances. Experiments demonstrate the topology-guided optimization results in better performance and faster convergence in many cases.
Unveiling Intrinsic Dimension of Texts: from Academic Abstract to Creative Story
Nov 19, 2025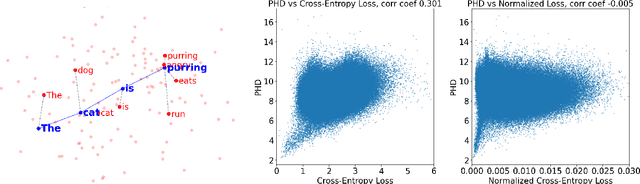
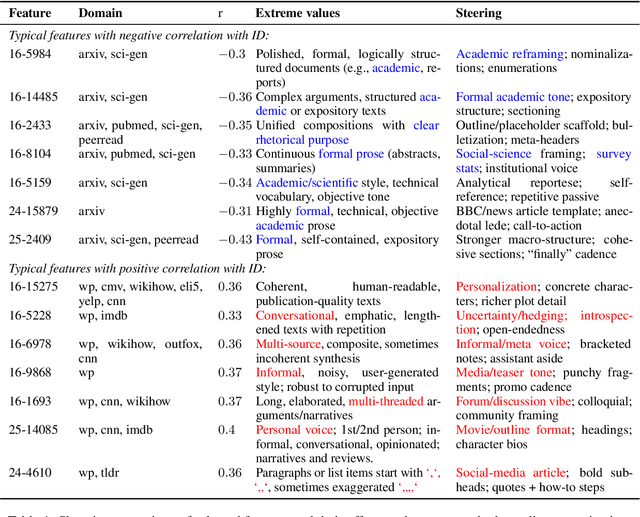
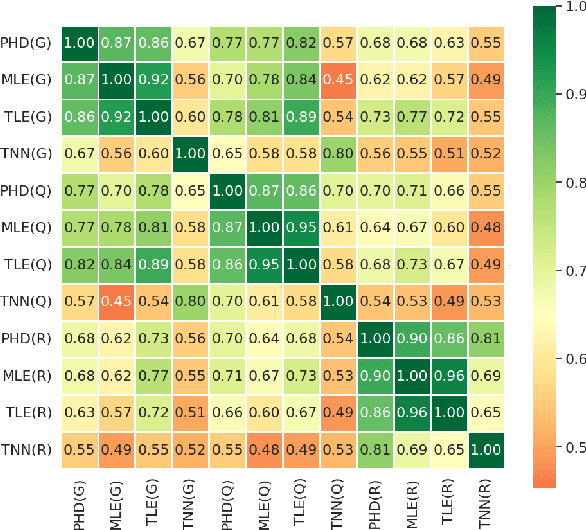

Abstract:Intrinsic dimension (ID) is an important tool in modern LLM analysis, informing studies of training dynamics, scaling behavior, and dataset structure, yet its textual determinants remain underexplored. We provide the first comprehensive study grounding ID in interpretable text properties through cross-encoder analysis, linguistic features, and sparse autoencoders (SAEs). In this work, we establish three key findings. First, ID is complementary to entropy-based metrics: after controlling for length, the two are uncorrelated, with ID capturing geometric complexity orthogonal to prediction quality. Second, ID exhibits robust genre stratification: scientific prose shows low ID (~8), encyclopedic content medium ID (~9), and creative/opinion writing high ID (~10.5) across all models tested. This reveals that contemporary LLMs find scientific text "representationally simple" while fiction requires additional degrees of freedom. Third, using SAEs, we identify causal features: scientific signals (formal tone, report templates, statistics) reduce ID; humanized signals (personalization, emotion, narrative) increase it. Steering experiments confirm these effects are causal. Thus, for contemporary models, scientific writing appears comparatively "easy", whereas fiction, opinion, and affect add representational degrees of freedom. Our multi-faceted analysis provides practical guidance for the proper use of ID and the sound interpretation of ID-based results.
RTD-Lite: Scalable Topological Analysis for Comparing Weighted Graphs in Learning Tasks
Mar 14, 2025Abstract:Topological methods for comparing weighted graphs are valuable in various learning tasks but often suffer from computational inefficiency on large datasets. We introduce RTD-Lite, a scalable algorithm that efficiently compares topological features, specifically connectivity or cluster structures at arbitrary scales, of two weighted graphs with one-to-one correspondence between vertices. Using minimal spanning trees in auxiliary graphs, RTD-Lite captures topological discrepancies with $O(n^2)$ time and memory complexity. This efficiency enables its application in tasks like dimensionality reduction and neural network training. Experiments on synthetic and real-world datasets demonstrate that RTD-Lite effectively identifies topological differences while significantly reducing computation time compared to existing methods. Moreover, integrating RTD-Lite into neural network training as a loss function component enhances the preservation of topological structures in learned representations. Our code is publicly available at https://github.com/ArGintum/RTD-Lite
Quantifying Logical Consistency in Transformers via Query-Key Alignment
Feb 24, 2025Abstract:Large language models (LLMs) have demonstrated impressive performance in various natural language processing tasks, yet their ability to perform multi-step logical reasoning remains an open challenge. Although Chain-of-Thought prompting has improved logical reasoning by enabling models to generate intermediate steps, it lacks mechanisms to assess the coherence of these logical transitions. In this paper, we propose a novel, lightweight evaluation strategy for logical reasoning that uses query-key alignments inside transformer attention heads. By computing a single forward pass and extracting a "QK-score" from carefully chosen heads, our method reveals latent representations that reliably separate valid from invalid inferences, offering a scalable alternative to traditional ablation-based techniques. We also provide an empirical validation on multiple logical reasoning benchmarks, demonstrating improved robustness of our evaluation method against distractors and increased reasoning depth. The experiments were conducted on a diverse set of models, ranging from 1.5B to 70B parameters.
Robust AI-Generated Text Detection by Restricted Embeddings
Oct 10, 2024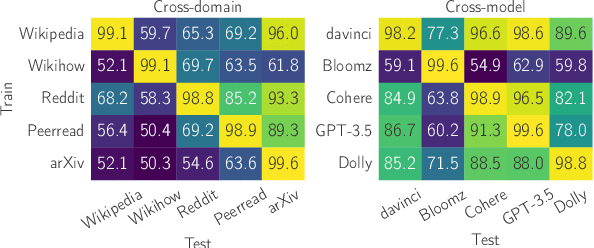
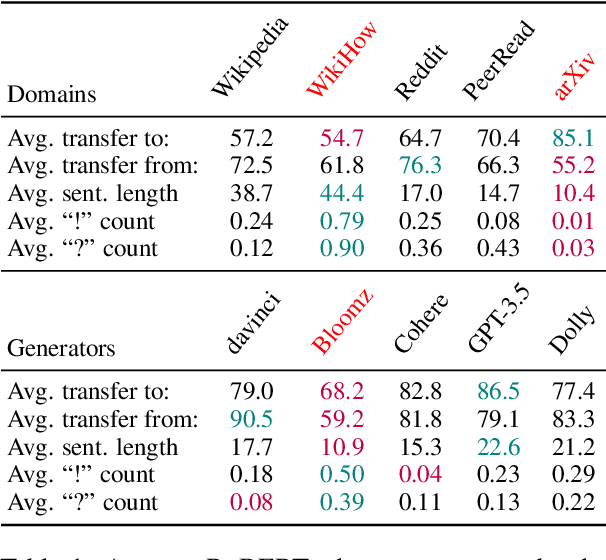
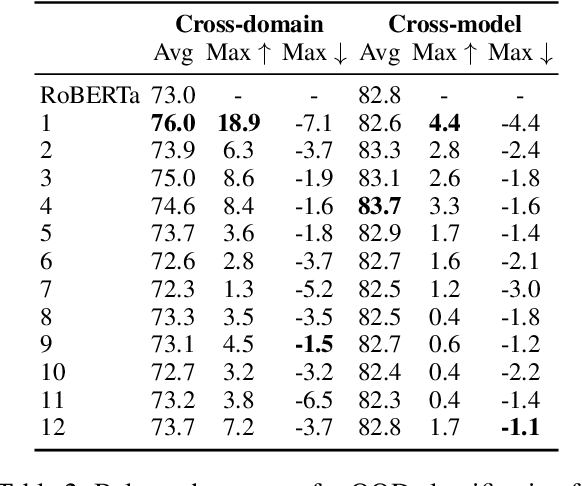
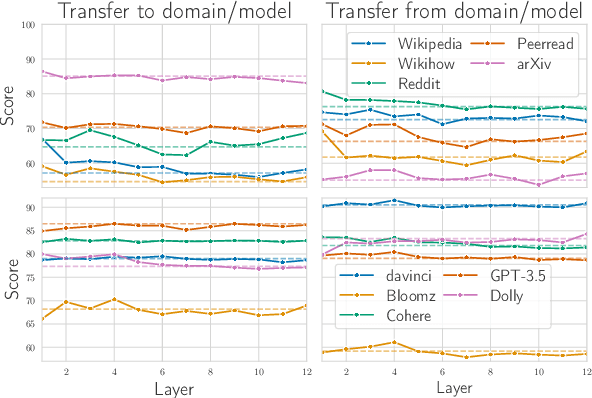
Abstract:Growing amount and quality of AI-generated texts makes detecting such content more difficult. In most real-world scenarios, the domain (style and topic) of generated data and the generator model are not known in advance. In this work, we focus on the robustness of classifier-based detectors of AI-generated text, namely their ability to transfer to unseen generators or semantic domains. We investigate the geometry of the embedding space of Transformer-based text encoders and show that clearing out harmful linear subspaces helps to train a robust classifier, ignoring domain-specific spurious features. We investigate several subspace decomposition and feature selection strategies and achieve significant improvements over state of the art methods in cross-domain and cross-generator transfer. Our best approaches for head-wise and coordinate-based subspace removal increase the mean out-of-distribution (OOD) classification score by up to 9% and 14% in particular setups for RoBERTa and BERT embeddings respectively. We release our code and data: https://github.com/SilverSolver/RobustATD
Listening to the Wise Few: Select-and-Copy Attention Heads for Multiple-Choice QA
Oct 03, 2024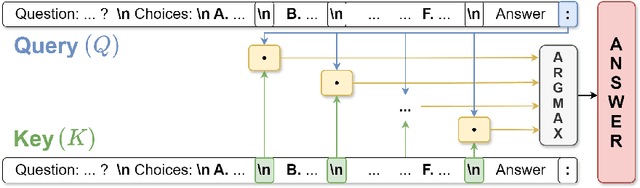
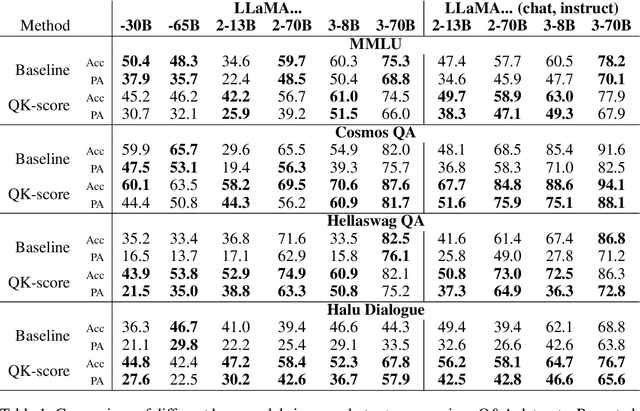
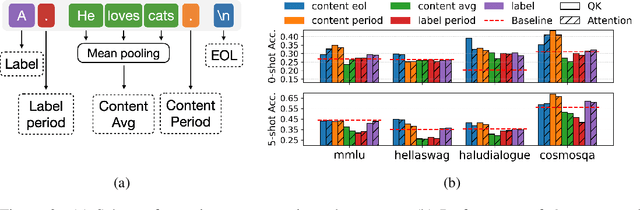
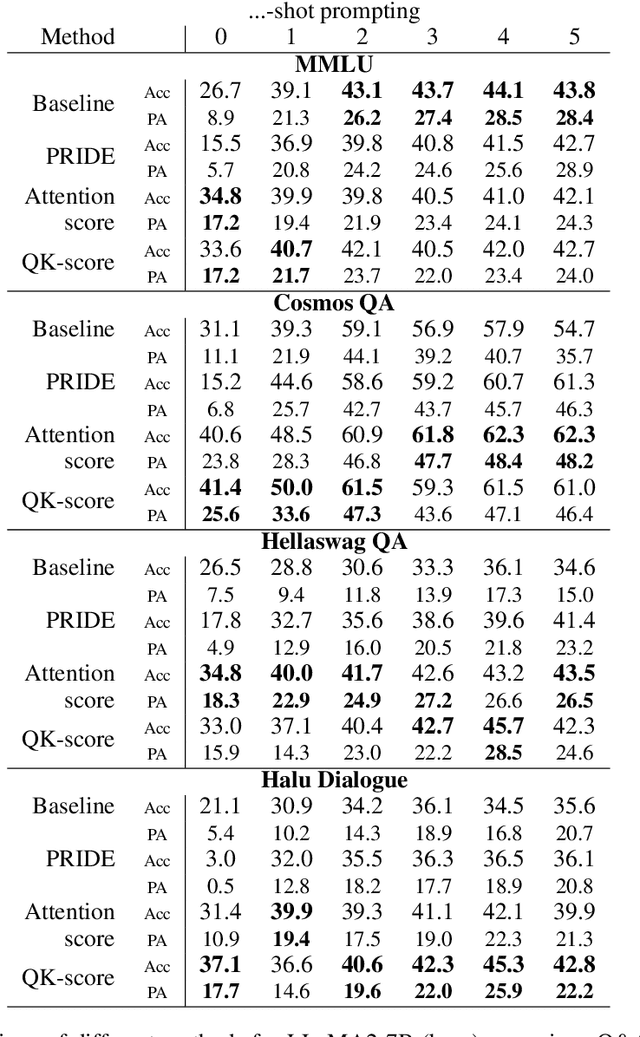
Abstract:A standard way to evaluate the abilities of LLM involves presenting a multiple-choice question and selecting the option with the highest logit as the model's predicted answer. However, such a format for evaluating LLMs has limitations, since even if the model knows the correct answer, it may struggle to select the corresponding letter simply due to difficulties in following this rigid format. To address this, we introduce new scores that better capture and reveal model's underlying knowledge: the Query-Key Score (QK-score), derived from the interaction between query and key representations in attention heads, and the Attention Score, based on attention weights. These scores are extracted from specific \textit{select-and-copy} heads, which show consistent performance across popular Multi-Choice Question Answering (MCQA) datasets. Based on these scores, our method improves knowledge extraction, yielding up to 16\% gain for LLaMA2-7B and up to 10\% for larger models on popular MCQA benchmarks. At the same time, the accuracy on a simple synthetic dataset, where the model explicitly knows the right answer, increases by almost 60\%, achieving nearly perfect accuracy, therefore demonstrating the method's efficiency in mitigating MCQA format limitations. To support our claims, we conduct experiments on models ranging from 7 billion to 70 billion parameters in both zero- and few-shot setups.
Scalar Function Topology Divergence: Comparing Topology of 3D Objects
Jul 11, 2024


Abstract:We propose a new topological tool for computer vision - Scalar Function Topology Divergence (SFTD), which measures the dissimilarity of multi-scale topology between sublevel sets of two functions having a common domain. Functions can be defined on an undirected graph or Euclidean space of any dimensionality. Most of the existing methods for comparing topology are based on Wasserstein distance between persistence barcodes and they don't take into account the localization of topological features. On the other hand, the minimization of SFTD ensures that the corresponding topological features of scalar functions are located in the same places. The proposed tool provides useful visualizations depicting areas where functions have topological dissimilarities. We provide applications of the proposed method to 3D computer vision. In particular, experiments demonstrate that SFTD improves the reconstruction of cellular 3D shapes from 2D fluorescence microscopy images, and helps to identify topological errors in 3D segmentation.
Intrinsic Dimension Estimation for Robust Detection of AI-Generated Texts
Jun 07, 2023



Abstract:Rapidly increasing quality of AI-generated content makes it difficult to distinguish between human and AI-generated texts, which may lead to undesirable consequences for society. Therefore, it becomes increasingly important to study the properties of human texts that are invariant over text domains and various proficiency of human writers, can be easily calculated for any language, and can robustly separate natural and AI-generated texts regardless of the generation model and sampling method. In this work, we propose such an invariant of human texts, namely the intrinsic dimensionality of the manifold underlying the set of embeddings of a given text sample. We show that the average intrinsic dimensionality of fluent texts in natural language is hovering around the value $9$ for several alphabet-based languages and around $7$ for Chinese, while the average intrinsic dimensionality of AI-generated texts for each language is $\approx 1.5$ lower, with a clear statistical separation between human-generated and AI-generated distributions. This property allows us to build a score-based artificial text detector. The proposed detector's accuracy is stable over text domains, generator models, and human writer proficiency levels, outperforming SOTA detectors in model-agnostic and cross-domain scenarios by a significant margin.
Learning Topology-Preserving Data Representations
Feb 15, 2023Abstract:We propose a method for learning topology-preserving data representations (dimensionality reduction). The method aims to provide topological similarity between the data manifold and its latent representation via enforcing the similarity in topological features (clusters, loops, 2D voids, etc.) and their localization. The core of the method is the minimization of the Representation Topology Divergence (RTD) between original high-dimensional data and low-dimensional representation in latent space. RTD minimization provides closeness in topological features with strong theoretical guarantees. We develop a scheme for RTD differentiation and apply it as a loss term for the autoencoder. The proposed method "RTD-AE" better preserves the global structure and topology of the data manifold than state-of-the-art competitors as measured by linear correlation, triplet distance ranking accuracy, and Wasserstein distance between persistence barcodes.
Topological Data Analysis for Speech Processing
Dec 02, 2022



Abstract:We apply topological data analysis (TDA) to speech classification problems and to the introspection of a pretrained speech model, HuBERT. To this end, we introduce a number of topological and algebraic features derived from Transformer attention maps and embeddings. We show that a simple linear classifier built on top of such features outperforms a fine-tuned classification head. In particular, we achieve an improvement of about $9\%$ accuracy and $5\%$ ERR on four common datasets; on CREMA-D, the proposed feature set reaches a new state of the art performance with accuracy $80.155$. We also show that topological features are able to reveal functional roles of speech Transformer heads; e.g., we find the heads capable to distinguish between pairs of sample sources (natural/synthetic) or voices without any downstream fine-tuning. Our results demonstrate that TDA is a promising new approach for speech analysis, especially for tasks that require structural prediction. Appendices, an introduction to TDA, and other additional materials are available here - https://topohubert.github.io/speech-topology-webpages/
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge