Daria Voronkova
Edge-wise Topological Divergence Gaps: Guiding Search in Combinatorial Optimization
Dec 16, 2025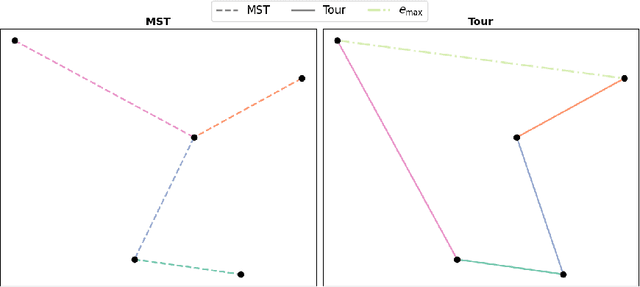
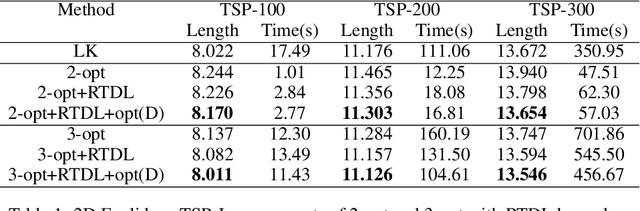
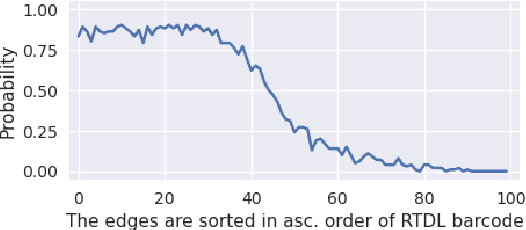
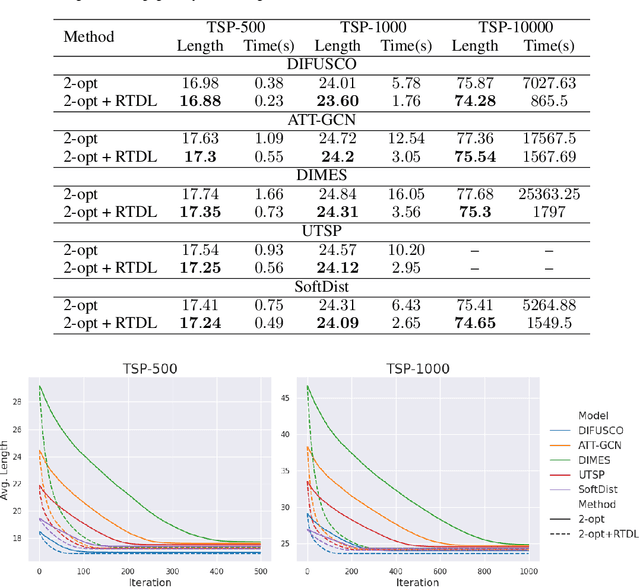
Abstract:We introduce a topological feedback mechanism for the Travelling Salesman Problem (TSP) by analyzing the divergence between a tour and the minimum spanning tree (MST). Our key contribution is a canonical decomposition theorem that expresses the tour-MST gap as edge-wise topology-divergence gaps from the RTD-Lite barcode. Based on this, we develop a topological guidance for 2-opt and 3-opt heuristics that increases their performance. We carry out experiments with fine-optimization of tours obtained from heatmap-based methods, TSPLIB, and random instances. Experiments demonstrate the topology-guided optimization results in better performance and faster convergence in many cases.
RTD-Lite: Scalable Topological Analysis for Comparing Weighted Graphs in Learning Tasks
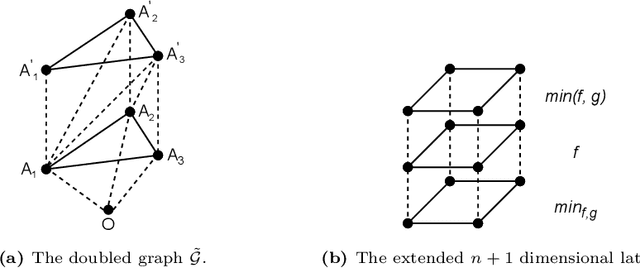
Mar 14, 2025Abstract:Topological methods for comparing weighted graphs are valuable in various learning tasks but often suffer from computational inefficiency on large datasets. We introduce RTD-Lite, a scalable algorithm that efficiently compares topological features, specifically connectivity or cluster structures at arbitrary scales, of two weighted graphs with one-to-one correspondence between vertices. Using minimal spanning trees in auxiliary graphs, RTD-Lite captures topological discrepancies with $O(n^2)$ time and memory complexity. This efficiency enables its application in tasks like dimensionality reduction and neural network training. Experiments on synthetic and real-world datasets demonstrate that RTD-Lite effectively identifies topological differences while significantly reducing computation time compared to existing methods. Moreover, integrating RTD-Lite into neural network training as a loss function component enhances the preservation of topological structures in learned representations. Our code is publicly available at https://github.com/ArGintum/RTD-Lite
Scalar Function Topology Divergence: Comparing Topology of 3D Objects
Jul 11, 2024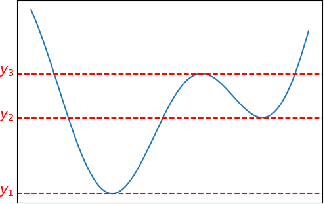


Abstract:We propose a new topological tool for computer vision - Scalar Function Topology Divergence (SFTD), which measures the dissimilarity of multi-scale topology between sublevel sets of two functions having a common domain. Functions can be defined on an undirected graph or Euclidean space of any dimensionality. Most of the existing methods for comparing topology are based on Wasserstein distance between persistence barcodes and they don't take into account the localization of topological features. On the other hand, the minimization of SFTD ensures that the corresponding topological features of scalar functions are located in the same places. The proposed tool provides useful visualizations depicting areas where functions have topological dissimilarities. We provide applications of the proposed method to 3D computer vision. In particular, experiments demonstrate that SFTD improves the reconstruction of cellular 3D shapes from 2D fluorescence microscopy images, and helps to identify topological errors in 3D segmentation.
Disentanglement Learning via Topology
Aug 24, 2023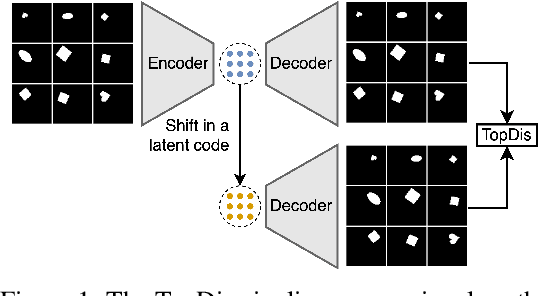
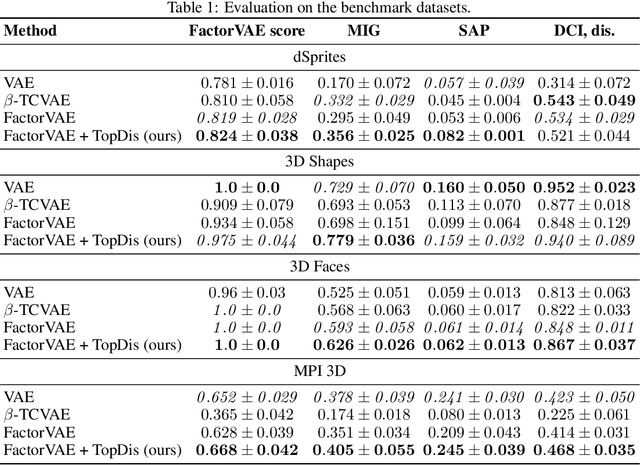
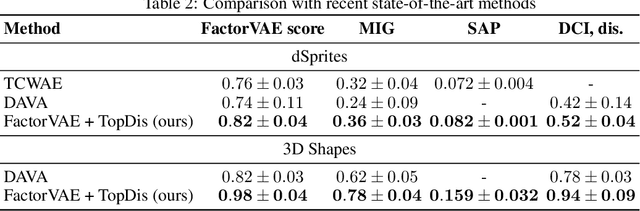
Abstract:We propose TopDis (Topological Disentanglement), a method for learning disentangled representations via adding multi-scale topological loss term. Disentanglement is a crucial property of data representations substantial for the explainability and robustness of deep learning models and a step towards high-level cognition. The state-of-the-art method based on VAE minimizes the total correlation of the joint distribution of latent variables. We take a different perspective on disentanglement by analyzing topological properties of data manifolds. In particular, we optimize the topological similarity for data manifolds traversals. To the best of our knowledge, our paper is the first one to propose a differentiable topological loss for disentanglement. Our experiments have shown that the proposed topological loss improves disentanglement scores such as MIG, FactorVAE score, SAP score and DCI disentanglement score with respect to state-of-the-art results. Our method works in an unsupervised manner, permitting to apply it for problems without labeled factors of variation. Additionally, we show how to use the proposed topological loss to find disentangled directions in a trained GAN.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge