FAS-RIS: A Block-Correlation Model Analysis

In this correspondence, we analyze the performance of a reconfigurable intelligent surface (RIS)-aided communication system that involves a fluid antenna system (FAS)-enabled receiver. By applying the central limit theorem (CLT), we derive approximate expressions for the system outage probability when the RIS has a large number of elements. Also, we adopt the block-correlation channel model to simplify the outage probability expressions, reducing the computational complexity and shedding light on the impact of the number of ports. Numerical results validate the effectiveness of our analysis, especially in scenarios with a large number of RIS elements.

A Tutorial on Fluid Antenna System for 6G Networks: Encompassing Communication Theory, Optimization Methods and Hardware Designs

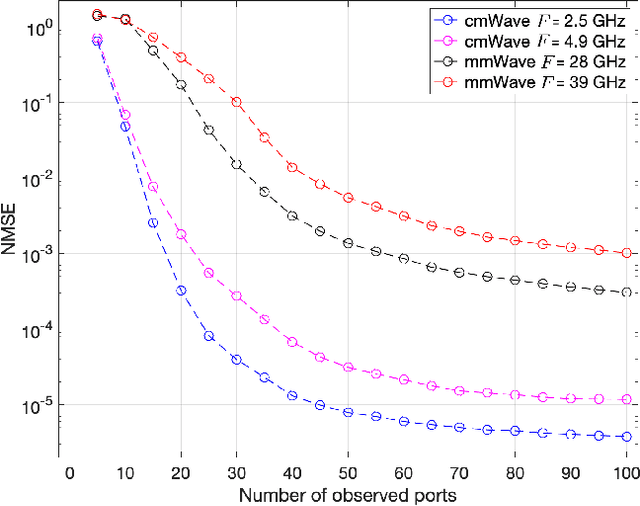
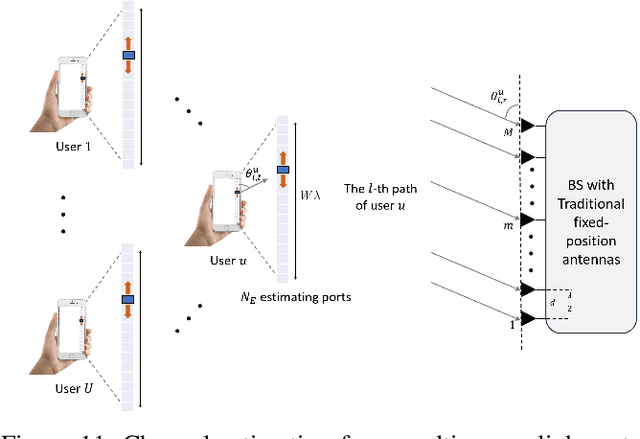
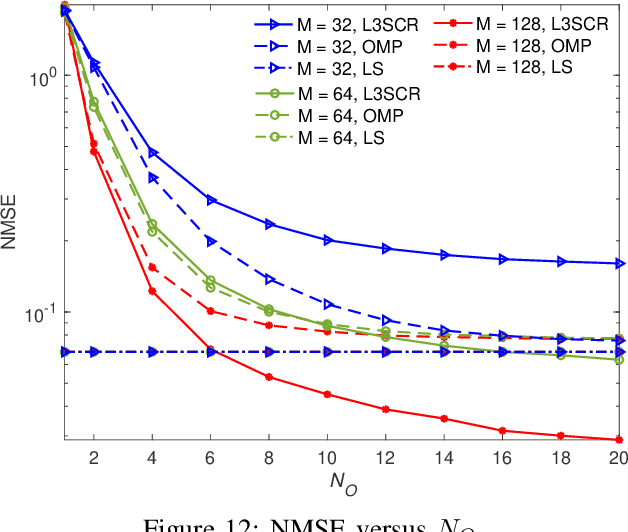
The advent of the sixth-generation (6G) networks presents another round of revolution for the mobile communication landscape, promising an immersive experience, robust reliability, minimal latency, extreme connectivity, ubiquitous coverage, and capabilities beyond communication, including intelligence and sensing. To achieve these ambitious goals, it is apparent that 6G networks need to incorporate the state-of-the-art technologies. One of the technologies that has garnered rising interest is fluid antenna system (FAS) which represents any software-controllable fluidic, conductive, or dielectric structure capable of dynamically changing its shape and position to reconfigure essential radio-frequency (RF) characteristics. Compared to traditional antenna systems (TASs) with fixed-position radiating elements, the core idea of FAS revolves around the unique flexibility of reconfiguring the radiating elements within a given space. One recent driver of FAS is the recognition of its position-flexibility as a new degree of freedom (dof) to harness diversity and multiplexing gains. In this paper, we provide a comprehensive tutorial, covering channel modeling, signal processing and estimation methods, information-theoretic insights, new multiple access techniques, and hardware designs. Moreover, we delineate the challenges of FAS and explore the potential of using FAS to improve the performance of other contemporary technologies. By providing insights and guidance, this tutorial paper serves to inspire researchers to explore new horizons and fully unleash the potential of FAS.

A New Spatial Block-Correlation Model for Fluid Antenna Systems

Powered by position-flexible antennas, the emerging fluid antenna system (FAS) technology postulates as a key enabler for massive connectivity in 6G networks. The free movement of antenna elements enables the opportunistic minimization of interference, allowing several users to share the same radio channel without the need of precoding. However, the true potential of FAS is still unknown due to the extremely high spatial correlation of the wireless channel between very close-by antenna positions. To unveil the multiplexing capabilities of FAS, proper (simple yet accurate) modeling of the spatial correlation is prominently needed. Realistic classical models such as Jakes' are prohibitively complex, rendering intractable analyses, while state-of-the-art approximations often are too simplistic and poorly accurate. Aiming to fill this gap, we here propose a general framework to approximate spatial correlation by block-diagonal matrices, motivated by the well-known block fading assumption and by statistical results on large correlation matrices. The proposed block-correlation model makes the performance analysis possible, and tightly approximates the results obtained with realistic models (Jakes' and Clarke's). Our framework is leveraged to analyze fluid antenna multiple access (FAMA) systems, evaluating their performance for both one- and two-dimensional fluid antennas.

Large Dimensional Analysis of Robust M-Estimators of Covariance with Outliers

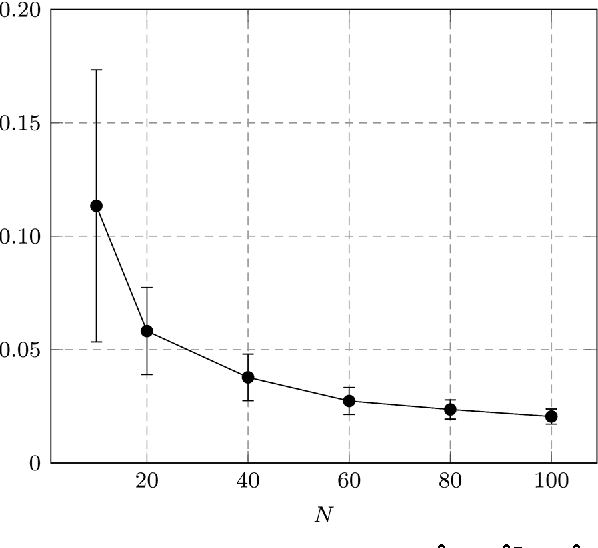
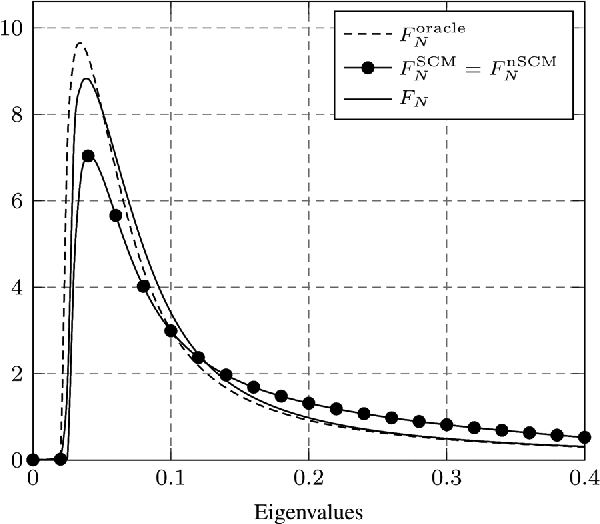
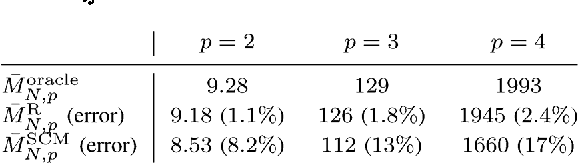
A large dimensional characterization of robust M-estimators of covariance (or scatter) is provided under the assumption that the dataset comprises independent (essentially Gaussian) legitimate samples as well as arbitrary deterministic samples, referred to as outliers. Building upon recent random matrix advances in the area of robust statistics, we specifically show that the so-called Maronna M-estimator of scatter asymptotically behaves similar to well-known random matrices when the population and sample sizes grow together to infinity. The introduction of outliers leads the robust estimator to behave asymptotically as the weighted sum of the sample outer products, with a constant weight for all legitimate samples and different weights for the outliers. A fine analysis of this structure reveals importantly that the propensity of the M-estimator to attenuate (or enhance) the impact of outliers is mostly dictated by the alignment of the outliers with the inverse population covariance matrix of the legitimate samples. Thus, robust M-estimators can bring substantial benefits over more simplistic estimators such as the per-sample normalized version of the sample covariance matrix, which is not capable of differentiating the outlying samples. The analysis shows that, within the class of Maronna's estimators of scatter, the Huber estimator is most favorable for rejecting outliers. On the contrary, estimators more similar to Tyler's scale invariant estimator (often preferred in the literature) run the risk of inadvertently enhancing some outliers.