Hypothesis Test Procedures for Detecting Leakage Signals in Water Pipeline Channels

We design statistical hypothesis tests for performing leak detection in water pipeline channels. By applying an appropriate model for signal propagation, we show that the detection problem becomes one of distinguishing signal from noise, with the noise being described by a multivariate Gaussian distribution with unknown covariance matrix. We first design a test procedure based on the generalized likelihood ratio test, which we show through simulations to offer appreciable leak detection performance gain over conventional approaches designed in an analogous context (for radar detection). Our proposed method requires estimation of the noise covariance matrix, which can become inaccurate under high-dimensional settings, and when the measurement data is scarce. To deal with this, we present a second leak detection method, which employs a regularized covariance matrix estimate. The regularization parameter is optimized for the leak detection application by applying results from large dimensional random matrix theory. This second proposed approach is shown to yield improved performance in leak detection compared with the first approach, at the expense of requiring higher computational complexity.

Optimal Grouping Strategy for Reconfigurable Intelligent Surface Assisted Wireless Communications

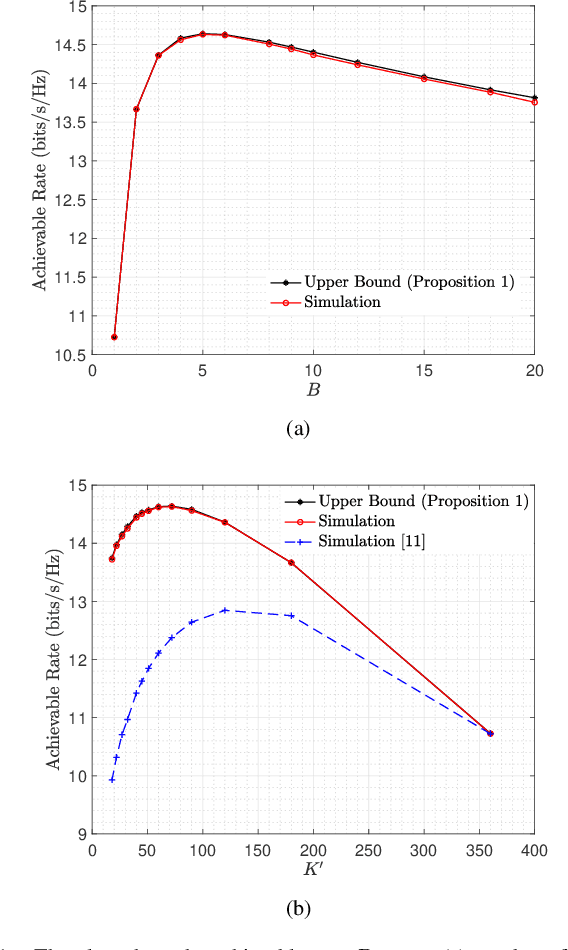
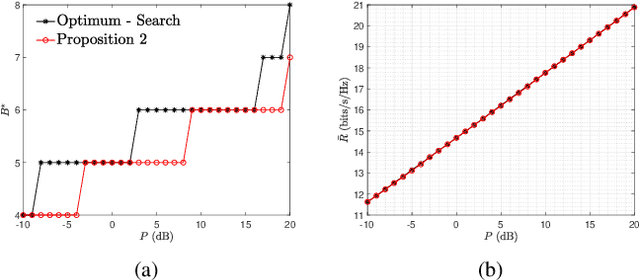
The channel estimation overhead of reconfigurable intelligent surface (RIS) assisted communication systems can be prohibitive. Prior works have demonstrated via simulations that grouping neighbouring RIS elements can help to reduce the pilot overhead and improve achievable rate. In this paper, we present an analytical study of RIS element grouping. We derive a tight closed-form upper bound for the achievable rate and then maximize it with respect to the group size. Our analysis reveals that more coarse-grained grouping is important-when the channel coherence time is low (high mobility scenarios) or the transmit power is large. We also demonstrate that optimal grouping can yield significant performance improvements over simple `On-Off' RIS element switching schemes that have been recently considered.

Machine Learning Based Parameter Estimation of Gaussian Quantum States

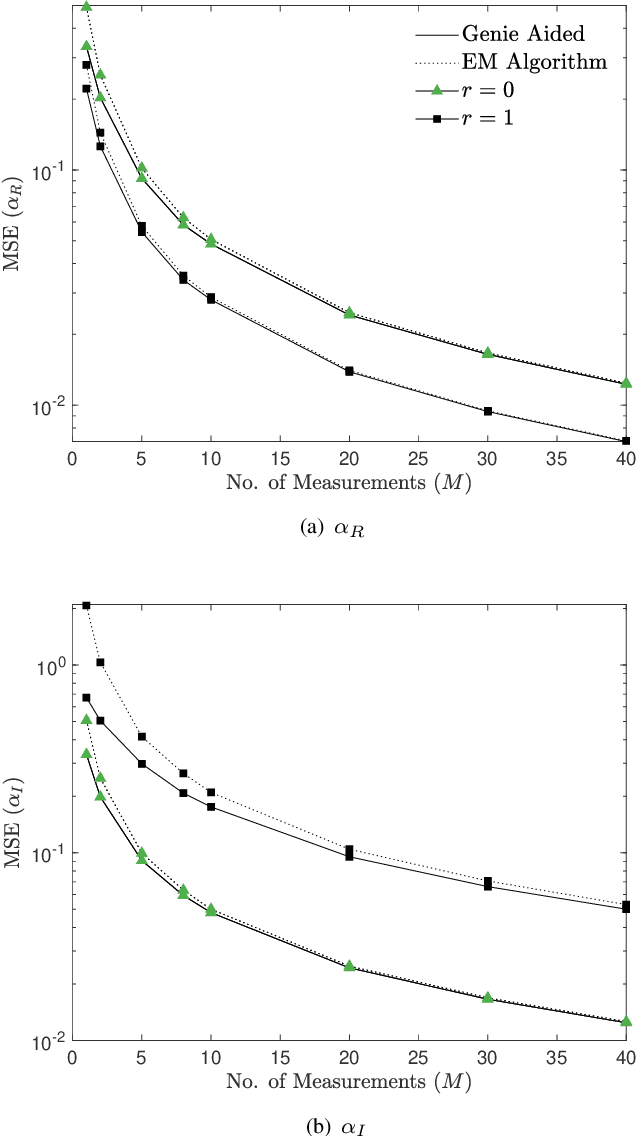
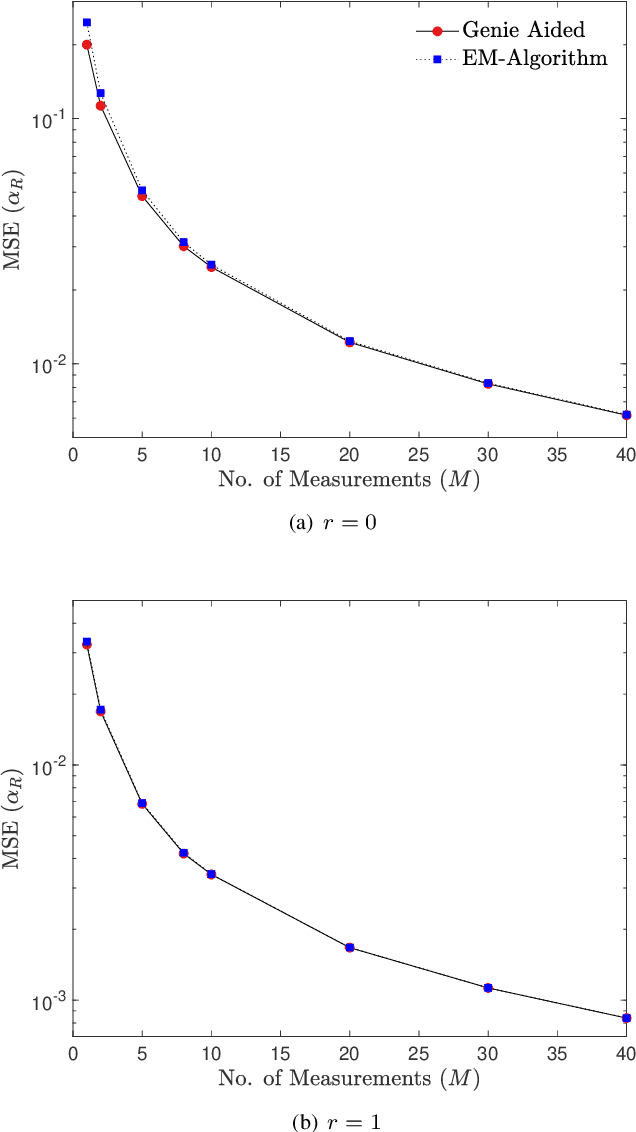
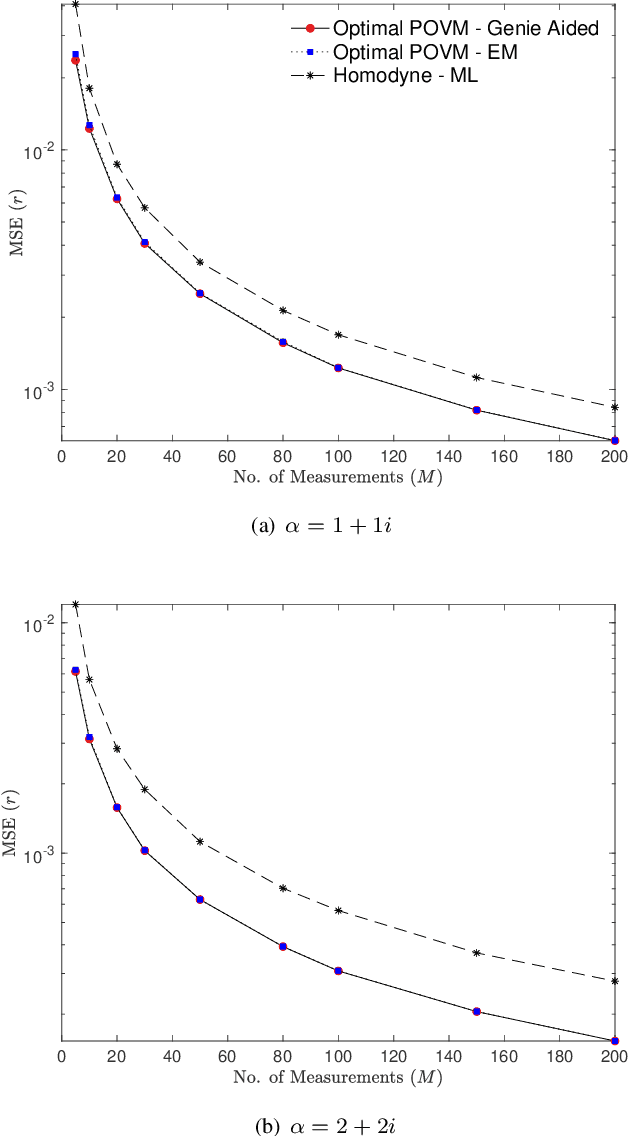
We propose a machine learning framework for parameter estimation of single mode Gaussian quantum states. Under a Bayesian framework, our approach estimates parameters of suitable prior distributions from measured data. For phase-space displacement and squeezing parameter estimation, this is achieved by introducing Expectation-Maximization (EM) based algorithms, while for phase parameter estimation an empirical Bayes method is applied. The estimated prior distribution parameters along with the observed data are used for finding the optimal Bayesian estimate of the unknown displacement, squeezing and phase parameters. Our simulation results show that the proposed algorithms have estimation performance that is very close to that of Genie Aided Bayesian estimators, that assume perfect knowledge of the prior parameters. Our proposed methods can be utilized by experimentalists to find the optimum Bayesian estimate of parameters of Gaussian quantum states by using only the observed measurements without requiring any knowledge about the prior distribution parameters.

MIMO Terahertz Quantum Key Distribution

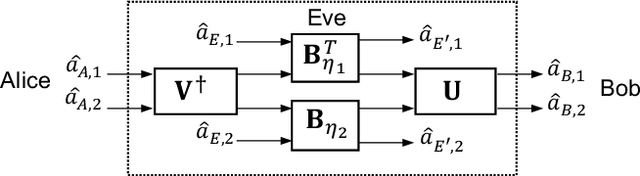
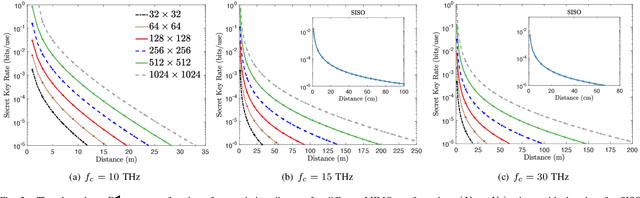
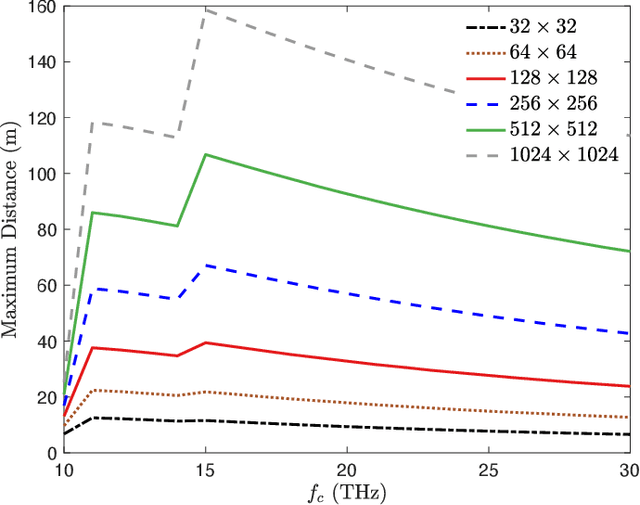
We propose a multiple-input multiple-output (MIMO) quantum key distribution (QKD) scheme for improving the secret key rates and increasing the maximum transmission distance for terahertz (THz) frequency range applications operating at room temperature. We propose a transmit beamforming and receive combining scheme that converts the rank-$r$ MIMO channel between Alice and Bob into $r$ parallel lossy quantum channels whose transmittances depend on the non-zero singular values of the MIMO channel. The MIMO transmission scheme provides a multiplexing gain of $r$, along with a beamforming and array gain equal to the product of the number of transmit and receive antennas. This improves the secret key rate and extends the maximum transmission distance. Our simulation results show that multiple antennas are necessary to overcome the high free-space path loss at THz frequencies. Positive key rates are achievable in the $10-30$ THz frequency range that can be used for both indoor and outdoor QKD applications for beyond fifth generation ultra-secure wireless communications systems.

Large Dimensional Analysis of Robust M-Estimators of Covariance with Outliers

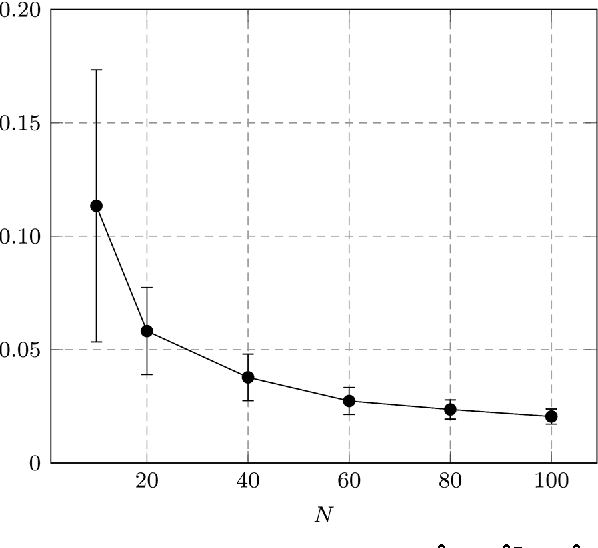
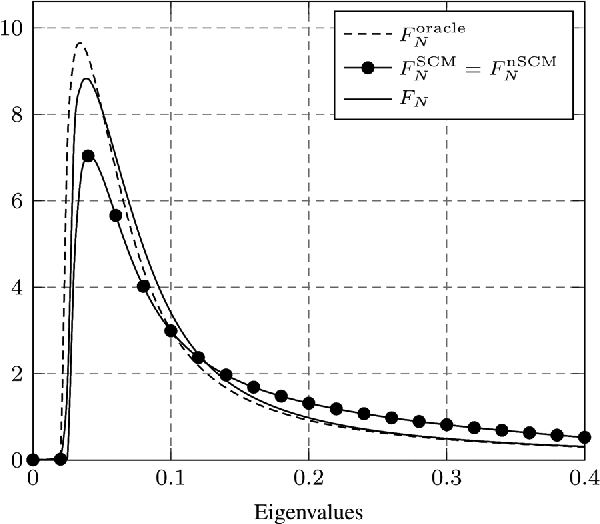
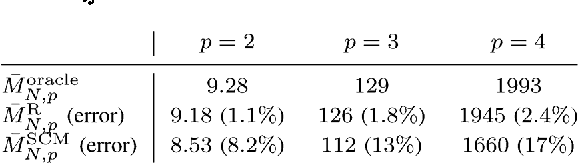
A large dimensional characterization of robust M-estimators of covariance (or scatter) is provided under the assumption that the dataset comprises independent (essentially Gaussian) legitimate samples as well as arbitrary deterministic samples, referred to as outliers. Building upon recent random matrix advances in the area of robust statistics, we specifically show that the so-called Maronna M-estimator of scatter asymptotically behaves similar to well-known random matrices when the population and sample sizes grow together to infinity. The introduction of outliers leads the robust estimator to behave asymptotically as the weighted sum of the sample outer products, with a constant weight for all legitimate samples and different weights for the outliers. A fine analysis of this structure reveals importantly that the propensity of the M-estimator to attenuate (or enhance) the impact of outliers is mostly dictated by the alignment of the outliers with the inverse population covariance matrix of the legitimate samples. Thus, robust M-estimators can bring substantial benefits over more simplistic estimators such as the per-sample normalized version of the sample covariance matrix, which is not capable of differentiating the outlying samples. The analysis shows that, within the class of Maronna's estimators of scatter, the Huber estimator is most favorable for rejecting outliers. On the contrary, estimators more similar to Tyler's scale invariant estimator (often preferred in the literature) run the risk of inadvertently enhancing some outliers.