Efficient Quantum Gradient and Higher-order Derivative Estimation via Generalized Hadamard Test

In the context of Noisy Intermediate-Scale Quantum (NISQ) computing, parameterized quantum circuits (PQCs) represent a promising paradigm for tackling challenges in quantum sensing, optimal control, optimization, and machine learning on near-term quantum hardware. Gradient-based methods are crucial for understanding the behavior of PQCs and have demonstrated substantial advantages in the convergence rates of Variational Quantum Algorithms (VQAs) compared to gradient-free methods. However, existing gradient estimation methods, such as Finite Difference, Parameter Shift Rule, Hadamard Test, and Direct Hadamard Test, often yield suboptimal gradient circuits for certain PQCs. To address these limitations, we introduce the Flexible Hadamard Test, which, when applied to first-order gradient estimation methods, can invert the roles of ansatz generators and observables. This inversion facilitates the use of measurement optimization techniques to efficiently compute PQC gradients. Additionally, to overcome the exponential cost of evaluating higher-order partial derivatives, we propose the $k$-fold Hadamard Test, which computes the $k^{th}$-order partial derivative using a single circuit. Furthermore, we introduce Quantum Automatic Differentiation (QAD), a unified gradient method that adaptively selects the best gradient estimation technique for individual parameters within a PQC. This represents the first implementation, to our knowledge, that departs from the conventional practice of uniformly applying a single method to all parameters. Through rigorous numerical experiments, we demonstrate the effectiveness of our proposed first-order gradient methods, showing up to an $O(N)$ factor improvement in circuit execution count for real PQC applications. Our research contributes to the acceleration of VQA computations, offering practical utility in the NISQ era of quantum computing.

Personalized Heart Disease Detection via ECG Digital Twin Generation

Heart diseases rank among the leading causes of global mortality, demonstrating a crucial need for early diagnosis and intervention. Most traditional electrocardiogram (ECG) based automated diagnosis methods are trained at population level, neglecting the customization of personalized ECGs to enhance individual healthcare management. A potential solution to address this limitation is to employ digital twins to simulate symptoms of diseases in real patients. In this paper, we present an innovative prospective learning approach for personalized heart disease detection, which generates digital twins of healthy individuals' anomalous ECGs and enhances the model sensitivity to the personalized symptoms. In our approach, a vector quantized feature separator is proposed to locate and isolate the disease symptom and normal segments in ECG signals with ECG report guidance. Thus, the ECG digital twins can simulate specific heart diseases used to train a personalized heart disease detection model. Experiments demonstrate that our approach not only excels in generating high-fidelity ECG signals but also improves personalized heart disease detection. Moreover, our approach ensures robust privacy protection, safeguarding patient data in model development.

Transformer-QEC: Quantum Error Correction Code Decoding with Transferable Transformers

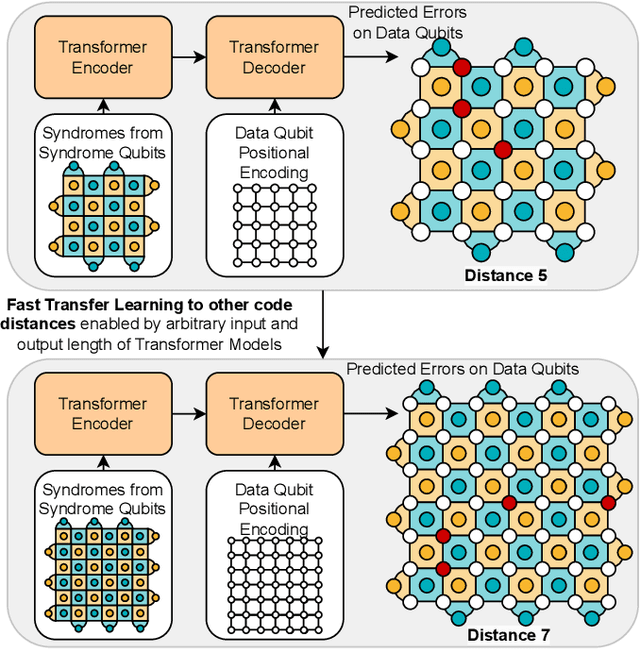
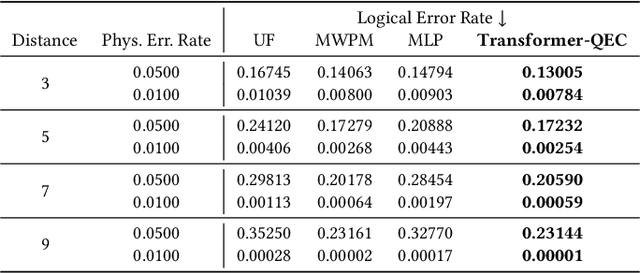
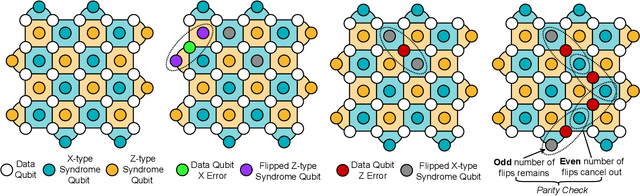
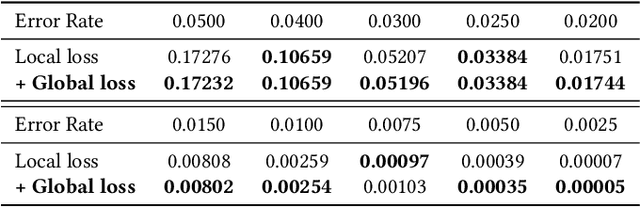
Quantum computing has the potential to solve problems that are intractable for classical systems, yet the high error rates in contemporary quantum devices often exceed tolerable limits for useful algorithm execution. Quantum Error Correction (QEC) mitigates this by employing redundancy, distributing quantum information across multiple data qubits and utilizing syndrome qubits to monitor their states for errors. The syndromes are subsequently interpreted by a decoding algorithm to identify and correct errors in the data qubits. This task is complex due to the multiplicity of error sources affecting both data and syndrome qubits as well as syndrome extraction operations. Additionally, identical syndromes can emanate from different error sources, necessitating a decoding algorithm that evaluates syndromes collectively. Although machine learning (ML) decoders such as multi-layer perceptrons (MLPs) and convolutional neural networks (CNNs) have been proposed, they often focus on local syndrome regions and require retraining when adjusting for different code distances. We introduce a transformer-based QEC decoder which employs self-attention to achieve a global receptive field across all input syndromes. It incorporates a mixed loss training approach, combining both local physical error and global parity label losses. Moreover, the transformer architecture's inherent adaptability to variable-length inputs allows for efficient transfer learning, enabling the decoder to adapt to varying code distances without retraining. Evaluation on six code distances and ten different error configurations demonstrates that our model consistently outperforms non-ML decoders, such as Union Find (UF) and Minimum Weight Perfect Matching (MWPM), and other ML decoders, thereby achieving best logical error rates. Moreover, the transfer learning can save over 10x of training cost.

Measuring incompatibility and clustering quantum observables with a quantum switch

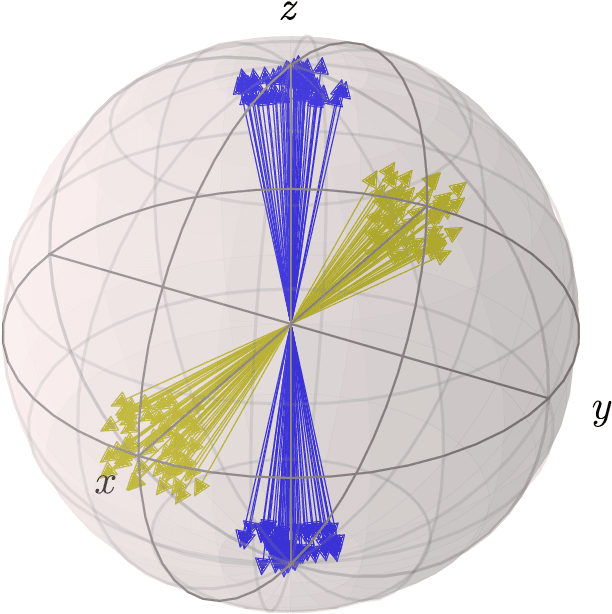
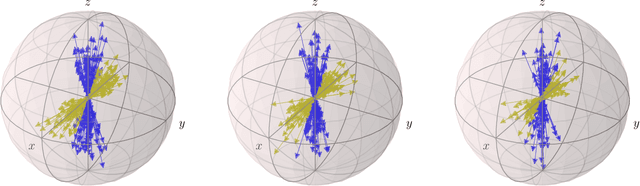
The existence of incompatible observables is a cornerstone of quantum mechanics and a valuable resource in quantum technologies. Here we introduce a measure of incompatibility, called the mutual eigenspace disturbance (MED), which quantifies the amount of disturbance induced by the measurement of a sharp observable on the eigenspaces of another. The MED is a faithful measure of incompatibility for sharp observables and provides a metric on the space of von Neumann measurements. It can be efficiently estimated by letting the measurements act in an indefinite order, using a setup known as the quantum switch. Thanks to these features, the MED can be used in quantum machine learning tasks, such as clustering quantum measurement devices based on their mutual compatibility. We demonstrate this application by providing an unsupervised algorithm that clusters unknown von Neumann measurements. Our algorithm is robust to noise can be used to identify groups of observers that share approximately the same measurement context.