Deepfake Media Generation and Detection in the Generative AI Era: A Survey and Outlook

With the recent advancements in generative modeling, the realism of deepfake content has been increasing at a steady pace, even reaching the point where people often fail to detect manipulated media content online, thus being deceived into various kinds of scams. In this paper, we survey deepfake generation and detection techniques, including the most recent developments in the field, such as diffusion models and Neural Radiance Fields. Our literature review covers all deepfake media types, comprising image, video, audio and multimodal (audio-visual) content. We identify various kinds of deepfakes, according to the procedure used to alter or generate the fake content. We further construct a taxonomy of deepfake generation and detection methods, illustrating the important groups of methods and the domains where these methods are applied. Next, we gather datasets used for deepfake detection and provide updated rankings of the best performing deepfake detectors on the most popular datasets. In addition, we develop a novel multimodal benchmark to evaluate deepfake detectors on out-of-distribution content. The results indicate that state-of-the-art detectors fail to generalize to deepfake content generated by unseen deepfake generators. Finally, we propose future directions to obtain robust and powerful deepfake detectors. Our project page and new benchmark are available at https://github.com/CroitoruAlin/biodeep.

Learning Explicitly Conditioned Sparsifying Transforms

Sparsifying transforms became in the last decades widely known tools for finding structured sparse representations of signals in certain transform domains. Despite the popularity of classical transforms such as DCT and Wavelet, learning optimal transforms that guarantee good representations of data into the sparse domain has been recently analyzed in a series of papers. Typically, the conditioning number and representation ability are complementary key features of learning square transforms that may not be explicitly controlled in a given optimization model. Unlike the existing approaches from the literature, in our paper, we consider a new sparsifying transform model that enforces explicit control over the data representation quality and the condition number of the learned transforms. We confirm through numerical experiments that our model presents better numerical behavior than the state-of-the-art.

Kernel t-distributed stochastic neighbor embedding

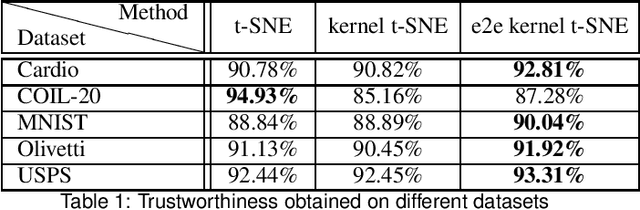
This paper presents a kernelized version of the t-SNE algorithm, capable of mapping high-dimensional data to a low-dimensional space while preserving the pairwise distances between the data points in a non-Euclidean metric. This can be achieved using a kernel trick only in the high dimensional space or in both spaces, leading to an end-to-end kernelized version. The proposed kernelized version of the t-SNE algorithm can offer new views on the relationships between data points, which can improve performance and accuracy in particular applications, such as classification problems involving kernel methods. The differences between t-SNE and its kernelized version are illustrated for several datasets, showing a neater clustering of points belonging to different classes.

Multidimensional orthogonal matching pursuit: theory and application to high accuracy joint localization and communication at mmWave

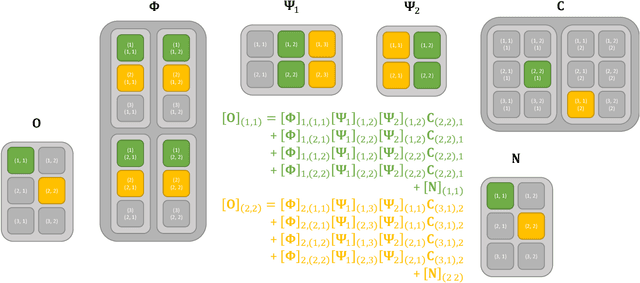
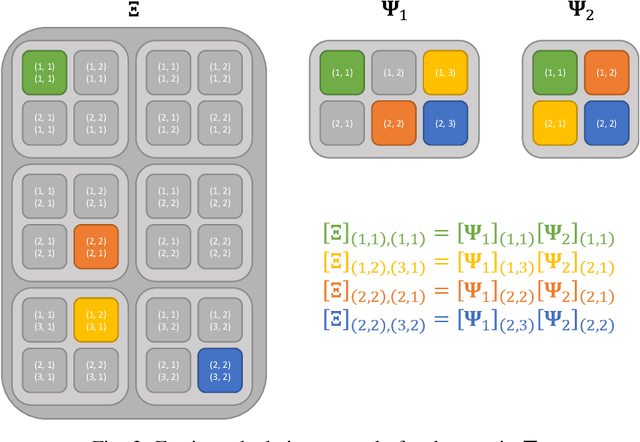
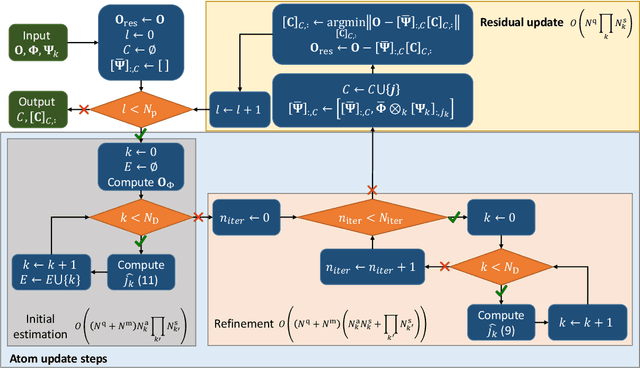
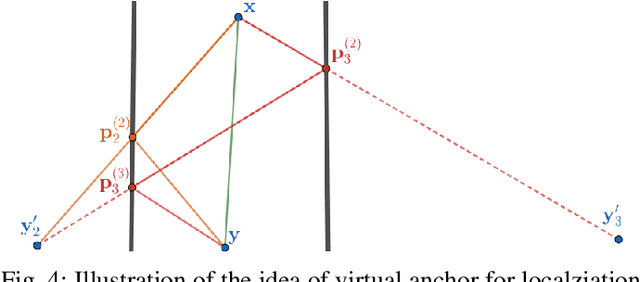
Greedy approaches in general, and orthogonal matching pursuit in particular, are the most commonly used sparse recovery techniques in a wide range of applications. The complexity of these approaches is highly dependent on the size of the dictionary chosen to represent the sparse signal. When the dictionary has to be large to enable high accuracy reconstructions, greedy strategies might however incur in prohibitive complexity. In this paper, we propose first the formulation of a new type of sparse recovery problems where the sparse signal is represented by a set of independent and smaller dictionaries instead of a large single one. Then, we derive a low complexity multdimensional orthogonal matching pursuit (MOMP) strategy for sparse recovery with a multdimensional dictionary. The projection step is performed iteratively on every dimension of the dictionary while fixing all other dimensions to achieve high accuracy estimation at a reasonable complexity. Finally, we formulate the problem of high resolution time domain channel estimation at millimeter wave (mmWave) frequencies as a multidimensional sparse recovery problem that can be solved with MOMP. The channel estimates are later transformed into high accuracy user position estimates exploiting a new localization algorithm that leverages the particular geometry of indoor channels. Simulation results show the effectiveness of MOMP for high accuracy localization at millimeter wave frequencies when operating in realistic 3D scenarios, with practical MIMO architectures feasible at mmWave, and without resorting to perfect synchronization assumptions that simplify the problem.

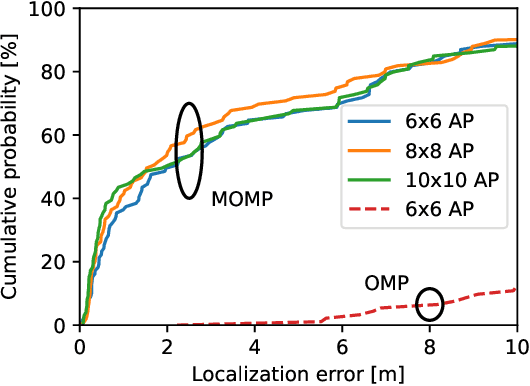
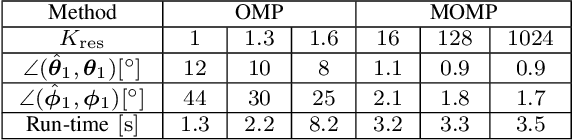
Low complexity joint position and channel estimation at millimeter wave based on multidimensional orthogonal matching pursuit

Compressive approaches provide a means of effective channel high resolution channel estimates in millimeter wave MIMO systems, despite the use of analog and hybrid architectures. Such estimates can also be used as part of a joint channel estimation and localization solution. Achieving good localization performance, though, requires high resolution channel estimates and better methods to exploit those channels. In this paper, we propose a low complexity multidimensional orthogonal matching pursuit strategy for compressive channel estimation based by operating with a product of independent dictionaries for the angular and delay domains, instead of a global large dictionary. This leads to higher quality channel estimates but with lower complexity than generalizations of conventional solutions. We couple this new algorithm with a novel localization formulation that does not rely on the absolute time of arrival of the LoS path and exploits the structure of reflections in indoor channels. We show how the new approach is able to operate in realistic 3D scenarios to estimate the communication channel and locate devices in an indoor simulation setting.

Dictionary Learning with Uniform Sparse Representations for Anomaly Detection

Many applications like audio and image processing show that sparse representations are a powerful and efficient signal modeling technique. Finding an optimal dictionary that generates at the same time the sparsest representations of data and the smallest approximation error is a hard problem approached by dictionary learning (DL). We study how DL performs in detecting abnormal samples in a dataset of signals. In this paper we use a particular DL formulation that seeks uniform sparse representations model to detect the underlying subspace of the majority of samples in a dataset, using a K-SVD-type algorithm. Numerical simulations show that one can efficiently use this resulted subspace to discriminate the anomalies over the regular data points.

An iterative coordinate descent algorithm to compute sparse low-rank approximations

In this paper, we describe a new algorithm to build a few sparse principal components from a given data matrix. Our approach does not explicitly create the covariance matrix of the data and can be viewed as an extension of the Kogbetliantz algorithm to build an approximate singular value decomposition for a few principal components. We show the performance of the proposed algorithm to recover sparse principal components on various datasets from the literature and perform dimensionality reduction for classification applications.

An iterative Jacobi-like algorithm to compute a few sparse eigenvalue-eigenvector pairs

In this paper, we describe a new algorithm to compute the extreme eigenvalue/eigenvector pairs of a symmetric matrix. The proposed algorithm can be viewed as an extension of the Jacobi transformation method for symmetric matrix diagonalization to the case where we want to compute just a few eigenvalues/eigenvectors. The method is also particularly well suited for the computation of sparse eigenspaces. We show the effectiveness of the method for sparse low-rank approximations and show applications to random symmetric matrices, graph Fourier transforms, and with the sparse principal component analysis in image classification experiments.

Efficient and Parallel Separable Dictionary Learning

Separable, or Kronecker product, dictionaries provide natural decompositions for 2D signals, such as images. In this paper, we describe an algorithm to learn such dictionaries which is highly parallelizable and which reaches sparse representations competitive with the previous state of the art dictionary learning algorithms from the literature. We highlight the performance of the proposed method to sparsely represent image data and for image denoising applications.

Constructing fast approximate eigenspaces with application to the fast graph Fourier transforms

We investigate numerically efficient approximations of eigenspaces associated to symmetric and general matrices. The eigenspaces are factored into a fixed number of fundamental components that can be efficiently manipulated (we consider extended orthogonal Givens or scaling and shear transformations). The number of these components controls the trade-off between approximation accuracy and the computational complexity of projecting on the eigenspaces. We write minimization problems for the single fundamental components and provide closed-form solutions. Then we propose algorithms that iterative update all these components until convergence. We show results on random matrices and an application on the approximation of graph Fourier transforms for directed and undirected graphs.