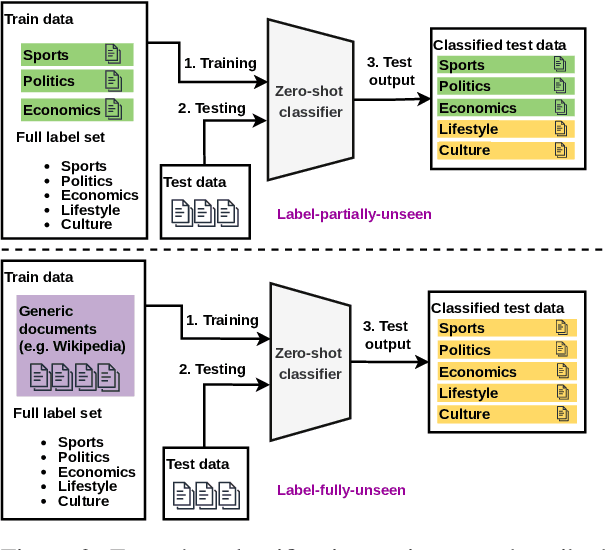
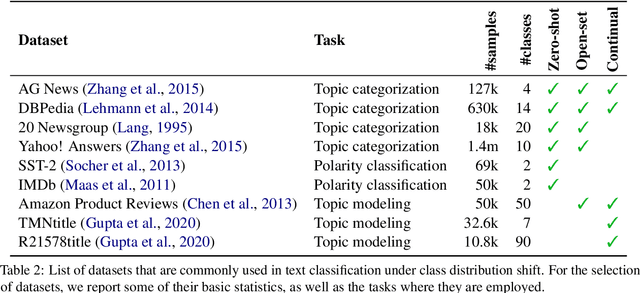
A Survey of Text Classification Under Class Distribution Shift

The basic underlying assumption of machine learning (ML) models is that the training and test data are sampled from the same distribution. However, in daily practice, this assumption is often broken, i.e.~the distribution of the test data changes over time, which hinders the application of conventional ML models. One domain where the distribution shift naturally occurs is text classification, since people always find new topics to discuss. To this end, we survey research articles studying open-set text classification and related tasks. We divide the methods in this area based on the constraints that define the kind of distribution shift and the corresponding problem formulation, i.e.~learning with the Universum, zero-shot learning, and open-set learning. We next discuss the predominant mitigation approaches for each problem setup. Finally, we identify several future work directions, aiming to push the boundaries beyond the state of the art. Interestingly, we find that continual learning can solve many of the issues caused by the shifting class distribution. We maintain a list of relevant papers at https://github.com/Eduard6421/Open-Set-Survey.

Dual Unscented Kalman Filter Architecture for Sensor Fusion in Water Networks Leak Localization

Leakage in water systems results in significant daily water losses, degrading service quality, increasing costs, and aggravating environmental problems. Most leak localization methods rely solely on pressure data, missing valuable information from other sensor types. This article proposes a hydraulic state estimation methodology based on a dual Unscented Kalman Filter (UKF) approach, which enhances the estimation of both nodal hydraulic heads, critical in localization tasks, and pipe flows, useful for operational purposes. The approach enables the fusion of different sensor types, such as pressure, flow and demand meters. The strategy is evaluated in well-known open source case studies, namely Modena and L-TOWN, showing improvements over other state-of-the-art estimation approaches in terms of interpolation accuracy, as well as more precise leak localization performance in L-TOWN.

Deepfake Media Generation and Detection in the Generative AI Era: A Survey and Outlook

With the recent advancements in generative modeling, the realism of deepfake content has been increasing at a steady pace, even reaching the point where people often fail to detect manipulated media content online, thus being deceived into various kinds of scams. In this paper, we survey deepfake generation and detection techniques, including the most recent developments in the field, such as diffusion models and Neural Radiance Fields. Our literature review covers all deepfake media types, comprising image, video, audio and multimodal (audio-visual) content. We identify various kinds of deepfakes, according to the procedure used to alter or generate the fake content. We further construct a taxonomy of deepfake generation and detection methods, illustrating the important groups of methods and the domains where these methods are applied. Next, we gather datasets used for deepfake detection and provide updated rankings of the best performing deepfake detectors on the most popular datasets. In addition, we develop a novel multimodal benchmark to evaluate deepfake detectors on out-of-distribution content. The results indicate that state-of-the-art detectors fail to generalize to deepfake content generated by unseen deepfake generators. Finally, we propose future directions to obtain robust and powerful deepfake detectors. Our project page and new benchmark are available at https://github.com/CroitoruAlin/biodeep.

Fusing Dictionary Learning and Support Vector Machines for Unsupervised Anomaly Detection

We study in this paper the improvement of one-class support vector machines (OC-SVM) through sparse representation techniques for unsupervised anomaly detection. As Dictionary Learning (DL) became recently a common analysis technique that reveals hidden sparse patterns of data, our approach uses this insight to endow unsupervised detection with more control on pattern finding and dimensions. We introduce a new anomaly detection model that unifies the OC-SVM and DL residual functions into a single composite objective, subsequently solved through K-SVD-type iterative algorithms. A closed-form of the alternating K-SVD iteration is explicitly derived for the new composite model and practical implementable schemes are discussed. The standard DL model is adapted for the Dictionary Pair Learning (DPL) context, where the usual sparsity constraints are naturally eliminated. Finally, we extend both objectives to the more general setting that allows the use of kernel functions. The empirical convergence properties of the resulting algorithms are provided and an in-depth analysis of their parametrization is performed while also demonstrating their numerical performance in comparison with existing methods.

Learning Explicitly Conditioned Sparsifying Transforms

Sparsifying transforms became in the last decades widely known tools for finding structured sparse representations of signals in certain transform domains. Despite the popularity of classical transforms such as DCT and Wavelet, learning optimal transforms that guarantee good representations of data into the sparse domain has been recently analyzed in a series of papers. Typically, the conditioning number and representation ability are complementary key features of learning square transforms that may not be explicitly controlled in a given optimization model. Unlike the existing approaches from the literature, in our paper, we consider a new sparsifying transform model that enforces explicit control over the data representation quality and the condition number of the learned transforms. We confirm through numerical experiments that our model presents better numerical behavior than the state-of-the-art.

Nodal Hydraulic Head Estimation through Unscented Kalman Filter for Data-driven Leak Localization in Water Networks

In this paper, we present a nodal hydraulic head estimation methodology for water distribution networks (WDN) based on an Unscented Kalman Filter (UKF) scheme with application to leak localization. The UKF refines an initial estimation of the hydraulic state by considering the prediction model, as well as available pressure and demand measurements. To this end, it provides customized prediction and data assimilation steps. Additionally, the method is enhanced by dynamically updating the prediction function weight matrices. Performance testing on the Modena benchmark under realistic conditions demonstrates the method's effectiveness in enhancing state estimation and data-driven leak localization.

Learning Dictionaries from Physical-Based Interpolation for Water Network Leak Localization

This article presents a leak localization methodology based on state estimation and learning. The first is handled by an interpolation scheme, whereas dictionary learning is considered for the second stage. The novel proposed interpolation technique exploits the physics of the interconnections between hydraulic heads of neighboring nodes in water distribution networks. Additionally, residuals are directly interpolated instead of hydraulic head values. The results of applying the proposed method to a well-known case study (Modena) demonstrated the improvements of the new interpolation method with respect to a state-of-the-art approach, both in terms of interpolation error (considering state and residual estimation) and posterior localization.

Unsupervised Abnormal Traffic Detection through Topological Flow Analysis

Cyberthreats are a permanent concern in our modern technological world. In the recent years, sophisticated traffic analysis techniques and anomaly detection (AD) algorithms have been employed to face the more and more subversive adversarial attacks. A malicious intrusion, defined as an invasive action intending to illegally exploit private resources, manifests through unusual data traffic and/or abnormal connectivity pattern. Despite the plethora of statistical or signature-based detectors currently provided in the literature, the topological connectivity component of a malicious flow is less exploited. Furthermore, a great proportion of the existing statistical intrusion detectors are based on supervised learning, that relies on labeled data. By viewing network flows as weighted directed interactions between a pair of nodes, in this paper we present a simple method that facilitate the use of connectivity graph features in unsupervised anomaly detection algorithms. We test our methodology on real network traffic datasets and observe several improvements over standard AD.

Dictionary Learning with Uniform Sparse Representations for Anomaly Detection

Many applications like audio and image processing show that sparse representations are a powerful and efficient signal modeling technique. Finding an optimal dictionary that generates at the same time the sparsest representations of data and the smallest approximation error is a hard problem approached by dictionary learning (DL). We study how DL performs in detecting abnormal samples in a dataset of signals. In this paper we use a particular DL formulation that seeks uniform sparse representations model to detect the underlying subspace of the majority of samples in a dataset, using a K-SVD-type algorithm. Numerical simulations show that one can efficiently use this resulted subspace to discriminate the anomalies over the regular data points.

Data-driven Leak Localization in Water Distribution Networks via Dictionary Learning and Graph-based Interpolation

In this paper, we propose a data-driven leak localization method for water distribution networks (WDNs) which combines two complementary approaches: graph-based interpolation and dictionary classification. The former estimates the complete WDN hydraulic state (i.e., hydraulic heads) from real measurements at certain nodes and the network graph. Then, these actual measurements, together with a subset of valuable estimated states, are used to feed and train the dictionary learning scheme. Thus, the meshing of these two methods is explored, showing that its performance is superior to either approach alone, even deriving different mechanisms to increase its resilience to classical problems (e.g., dimensionality, interpolation errors, etc.). The approach is validated using the L-TOWN benchmark proposed at BattLeDIM2020.