Haar-Laplacian for directed graphs

This paper introduces a novel Laplacian matrix aiming to enable the construction of spectral convolutional networks and to extend the signal processing applications for directed graphs. Our proposal is inspired by a Haar-like transformation and produces a Hermitian matrix which is not only in one-to-one relation with the adjacency matrix, preserving both direction and weight information, but also enjoys desirable additional properties like scaling robustness, sensitivity, continuity, and directionality. We take a theoretical standpoint and support the conformity of our approach with the spectral graph theory. Then, we address two use-cases: graph learning (by introducing HaarNet, a spectral graph convolutional network built with our Haar-Laplacian) and graph signal processing. We show that our approach gives better results in applications like weight prediction and denoising on directed graphs.

Atom dimension adaptation for infinite set dictionary learning

Recent work on dictionary learning with set-atoms has shown benefits in anomaly detection. Instead of viewing an atom as a single vector, these methods allow building sparse representations with atoms taken from a set around a central vector; the set can be a cone or may have a probability distribution associated to it. We propose a method for adaptively adjusting the size of set-atoms in Gaussian and cone dictionary learning. The purpose of the algorithm is to match the atom sizes with their contribution in representing the signals. The proposed algorithm not only decreases the representation error, but also improves anomaly detection, for a class of anomalies called `dependency'. We obtain better detection performance than state-of-the-art methods.

Reduced Kernel Dictionary Learning

In this paper we present new algorithms for training reduced-size nonlinear representations in the Kernel Dictionary Learning (KDL) problem. Standard KDL has the drawback of a large size of the kernel matrix when the data set is large. There are several ways of reducing the kernel size, notably Nystr\"om sampling. We propose here a method more in the spirit of dictionary learning, where the kernel vectors are obtained with a trained sparse representation of the input signals. Moreover, we optimize directly the kernel vectors in the KDL process, using gradient descent steps. We show with three data sets that our algorithms are able to provide better representations, despite using a small number of kernel vectors, and also decrease the execution time with respect to KDL.

Classification with Incoherent Kernel Dictionary Learning

In this paper we present a new classification method based on Dictionary Learning (DL). The main contribution consists of a kernel version of incoherent DL, derived from its standard linear counterpart. We also propose an improvement of the AK-SVD algorithm concerning the representation update. Our algorithms are tested on several popular databases of classification problems.

Anomaly Detection with Selective Dictionary Learning

In this paper we present new methods of anomaly detection based on Dictionary Learning (DL) and Kernel Dictionary Learning (KDL). The main contribution consists in the adaption of known DL and KDL algorithms in the form of unsupervised methods, used for outlier detection. We propose a reduced kernel version (RKDL), which is useful for problems with large data sets, due to the large kernel matrix. We also improve the DL and RKDL methods by the use of a random selection of signals, which aims to eliminate the outliers from the training procedure. All our algorithms are introduced in an anomaly detection toolbox and are compared to standard benchmark results.

Kernel t-distributed stochastic neighbor embedding

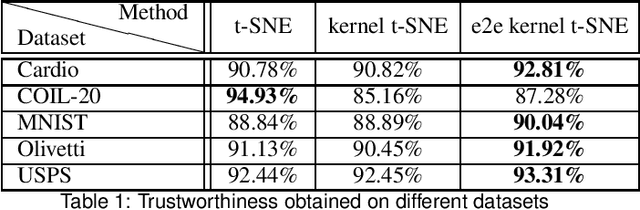
This paper presents a kernelized version of the t-SNE algorithm, capable of mapping high-dimensional data to a low-dimensional space while preserving the pairwise distances between the data points in a non-Euclidean metric. This can be achieved using a kernel trick only in the high dimensional space or in both spaces, leading to an end-to-end kernelized version. The proposed kernelized version of the t-SNE algorithm can offer new views on the relationships between data points, which can improve performance and accuracy in particular applications, such as classification problems involving kernel methods. The differences between t-SNE and its kernelized version are illustrated for several datasets, showing a neater clustering of points belonging to different classes.

Deep recommender engine based on efficient product embeddings neural pipeline

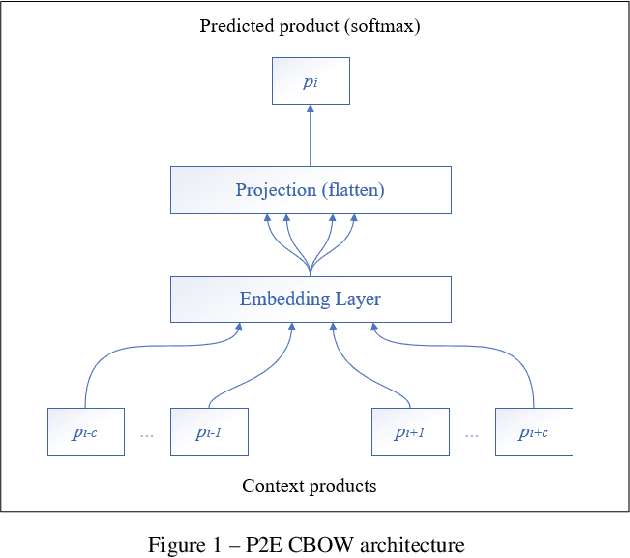
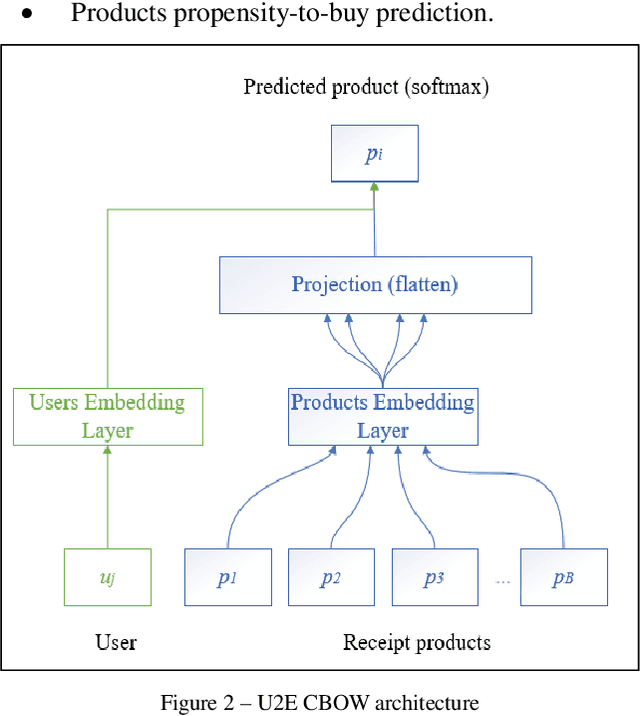
Predictive analytics systems are currently one of the most important areas of research and development within the Artificial Intelligence domain and particularly in Machine Learning. One of the "holy grails" of predictive analytics is the research and development of the "perfect" recommendation system. In our paper we propose an advanced pipeline model for the multi-task objective of determining product complementarity, similarity and sales prediction using deep neural models applied to big-data sequential transaction systems. Our highly parallelized hybrid pipeline consists of both unsupervised and supervised models, used for the objectives of generating semantic product embeddings and predicting sales, respectively. Our experimentation and benchmarking have been done using very large pharma-industry retailer Big Data stream.

Overcomplete Dictionary Learning with Jacobi Atom Updates

Dictionary learning for sparse representations is traditionally approached with sequential atom updates, in which an optimized atom is used immediately for the optimization of the next atoms. We propose instead a Jacobi version, in which groups of atoms are updated independently, in parallel. Extensive numerical evidence for sparse image representation shows that the parallel algorithms, especially when all atoms are updated simultaneously, give better dictionaries than their sequential counterparts.