Nonlinear Neural Dynamics and Classification Accuracy in Reservoir Computing

Reservoir computing - information processing based on untrained recurrent neural networks with random connections - is expected to depend on the nonlinear properties of the neurons and the resulting oscillatory, chaotic, or fixpoint dynamics of the network. However, the required degree of nonlinearity and the range of suitable dynamical regimes for a given task are not fully understood. To clarify these questions, we study the accuracy of a reservoir computer in artificial classification tasks of varying complexity, while tuning the neuron's degree of nonlinearity and the reservoir's dynamical regime. We find that, even for activation functions with extremely reduced nonlinearity, weak recurrent interactions and small input signals, the reservoir is able to compute useful representations, detectable only in higher order principal components, that render complex classificiation tasks linearly separable for the readout layer. When increasing the recurrent coupling, the reservoir develops spontaneous dynamical behavior. Nevertheless, the input-related computations can 'ride on top' of oscillatory or fixpoint attractors without much loss of accuracy, whereas chaotic dynamics reduces task performance more drastically. By tuning the system through the full range of dynamical phases, we find that the accuracy peaks both at the oscillatory/chaotic and at the chaotic/fixpoint phase boundaries, thus supporting the 'edge of chaos' hypothesis. Our results, in particular the robust weakly nonlinear operating regime, may offer new perspectives both for technical and biological neural networks with random connectivity.

Analyzing Narrative Processing in Large Language Models (LLMs): Using GPT4 to test BERT

The ability to transmit and receive complex information via language is unique to humans and is the basis of traditions, culture and versatile social interactions. Through the disruptive introduction of transformer based large language models (LLMs) humans are not the only entity to "understand" and produce language any more. In the present study, we have performed the first steps to use LLMs as a model to understand fundamental mechanisms of language processing in neural networks, in order to make predictions and generate hypotheses on how the human brain does language processing. Thus, we have used ChatGPT to generate seven different stylistic variations of ten different narratives (Aesop's fables). We used these stories as input for the open source LLM BERT and have analyzed the activation patterns of the hidden units of BERT using multi-dimensional scaling and cluster analysis. We found that the activation vectors of the hidden units cluster according to stylistic variations in earlier layers of BERT (1) than narrative content (4-5). Despite the fact that BERT consists of 12 identical building blocks that are stacked and trained on large text corpora, the different layers perform different tasks. This is a very useful model of the human brain, where self-similar structures, i.e. different areas of the cerebral cortex, can have different functions and are therefore well suited to processing language in a very efficient way. The proposed approach has the potential to open the black box of LLMs on the one hand, and might be a further step to unravel the neural processes underlying human language processing and cognition in general.

Beyond Labels: Advancing Cluster Analysis with the Entropy of Distance Distribution (EDD)

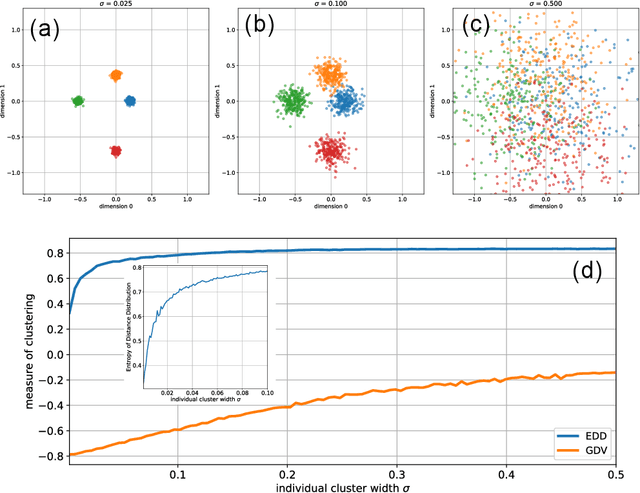
In the evolving landscape of data science, the accurate quantification of clustering in high-dimensional data sets remains a significant challenge, especially in the absence of predefined labels. This paper introduces a novel approach, the Entropy of Distance Distribution (EDD), which represents a paradigm shift in label-free clustering analysis. Traditional methods, reliant on discrete labels, often struggle to discern intricate cluster patterns in unlabeled data. EDD, however, leverages the characteristic differences in pairwise point-to-point distances to discern clustering tendencies, independent of data labeling. Our method employs the Shannon information entropy to quantify the 'peakedness' or 'flatness' of distance distributions in a data set. This entropy measure, normalized against its maximum value, effectively distinguishes between strongly clustered data (indicated by pronounced peaks in distance distribution) and more homogeneous, non-clustered data sets. This label-free quantification is resilient against global translations and permutations of data points, and with an additional dimension-wise z-scoring, it becomes invariant to data set scaling. We demonstrate the efficacy of EDD through a series of experiments involving two-dimensional data spaces with Gaussian cluster centers. Our findings reveal a monotonic increase in the EDD value with the widening of cluster widths, moving from well-separated to overlapping clusters. This behavior underscores the method's sensitivity and accuracy in detecting varying degrees of clustering. EDD's potential extends beyond conventional clustering analysis, offering a robust, scalable tool for unraveling complex data structures without reliance on pre-assigned labels.

Quantifying and maximizing the information flux in recurrent neural networks

Free-running Recurrent Neural Networks (RNNs), especially probabilistic models, generate an ongoing information flux that can be quantified with the mutual information $I\left[\vec{x}(t),\vec{x}(t\!+\!1)\right]$ between subsequent system states $\vec{x}$. Although, former studies have shown that $I$ depends on the statistics of the network's connection weights, it is unclear (1) how to maximize $I$ systematically and (2) how to quantify the flux in large systems where computing the mutual information becomes intractable. Here, we address these questions using Boltzmann machines as model systems. We find that in networks with moderately strong connections, the mutual information $I$ is approximately a monotonic transformation of the root-mean-square averaged Pearson correlations between neuron-pairs, a quantity that can be efficiently computed even in large systems. Furthermore, evolutionary maximization of $I\left[\vec{x}(t),\vec{x}(t\!+\!1)\right]$ reveals a general design principle for the weight matrices enabling the systematic construction of systems with a high spontaneous information flux. Finally, we simultaneously maximize information flux and the mean period length of cyclic attractors in the state space of these dynamical networks. Our results are potentially useful for the construction of RNNs that serve as short-time memories or pattern generators.

Classification at the Accuracy Limit -- Facing the Problem of Data Ambiguity

Data classification, the process of analyzing data and organizing it into categories, is a fundamental computing problem of natural and artificial information processing systems. Ideally, the performance of classifier models would be evaluated using unambiguous data sets, where the 'correct' assignment of category labels to the input data vectors is unequivocal. In real-world problems, however, a significant fraction of actually occurring data vectors will be located in a boundary zone between or outside of all categories, so that perfect classification cannot even in principle be achieved. We derive the theoretical limit for classification accuracy that arises from the overlap of data categories. By using a surrogate data generation model with adjustable statistical properties, we show that sufficiently powerful classifiers based on completely different principles, such as perceptrons and Bayesian models, all perform at this universal accuracy limit. Remarkably, the accuracy limit is not affected by applying non-linear transformations to the data, even if these transformations are non-reversible and drastically reduce the information content of the input data. We compare emerging data embeddings produced by supervised and unsupervised training, using MNIST and human EEG recordings during sleep. We find that categories are not only well separated in the final layers of classifiers trained with back-propagation, but to a smaller degree also after unsupervised dimensionality reduction. This suggests that human-defined categories, such as hand-written digits or sleep stages, can indeed be considered as 'natural kinds'.

Predictive Coding and Stochastic Resonance: Towards a Unified Theory of Auditory (Phantom) Perception

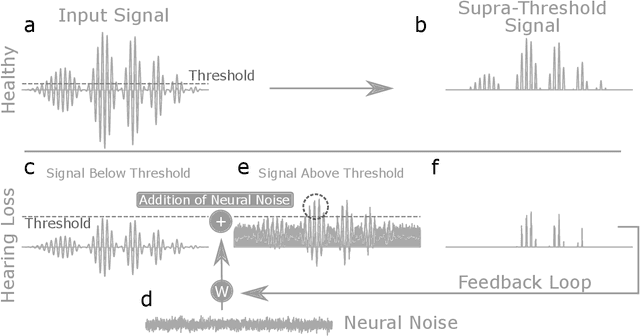
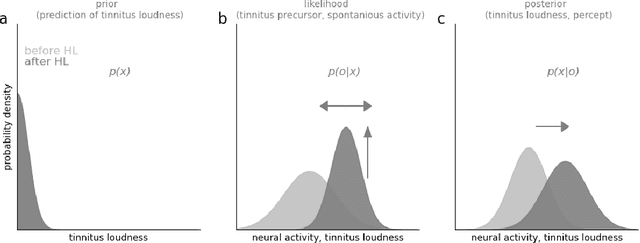
Cognitive computational neuroscience (CCN) suggests that to gain a mechanistic understanding of brain function, hypothesis driven experiments should be accompanied by biologically plausible computational models. This novel research paradigm offers a way from alchemy to chemistry, in auditory neuroscience. With a special focus on tinnitus - as the prime example of auditory phantom perception - we review recent work at the intersection of artificial intelligence, psychology, and neuroscience, foregrounding the idea that experiments will yield mechanistic insight only when employed to test formal or computational models. This view challenges the popular notion that tinnitus research is primarily data limited, and that producing large, multi-modal, and complex data-sets, analyzed with advanced data analysis algorithms, will lead to fundamental insights into how tinnitus emerges. We conclude that two fundamental processing principles - being ubiquitous in the brain - best fit to a vast number of experimental results and therefore provide the most explanatory power: predictive coding as a top-down, and stochastic resonance as a complementary bottom-up mechanism. Furthermore, we argue that even though contemporary artificial intelligence and machine learning approaches largely lack biological plausibility, the models to be constructed will have to draw on concepts from these fields; since they provide a formal account of the requisite computations that underlie brain function. Nevertheless, biological fidelity will have to be addressed, allowing for testing possible treatment strategies in silico, before application in animal or patient studies. This iteration of computational and empirical studies may help to open the "black boxes" of both machine learning and the human brain.

Neural Network based Successor Representations of Space and Language

How does the mind organize thoughts? The hippocampal-entorhinal complex is thought to support domain-general representation and processing of structural knowledge of arbitrary state, feature and concept spaces. In particular, it enables the formation of cognitive maps, and navigation on these maps, thereby broadly contributing to cognition. It has been proposed that the concept of multi-scale successor representations provides an explanation of the underlying computations performed by place and grid cells. Here, we present a neural network based approach to learn such representations, and its application to different scenarios: a spatial exploration task based on supervised learning, a spatial navigation task based on reinforcement learning, and a non-spatial task where linguistic constructions have to be inferred by observing sample sentences. In all scenarios, the neural network correctly learns and approximates the underlying structure by building successor representations. Furthermore, the resulting neural firing patterns are strikingly similar to experimentally observed place and grid cell firing patterns. We conclude that cognitive maps and neural network-based successor representations of structured knowledge provide a promising way to overcome some of the short comings of deep learning towards artificial general intelligence.

How deep is deep enough? - Optimizing deep neural network architecture

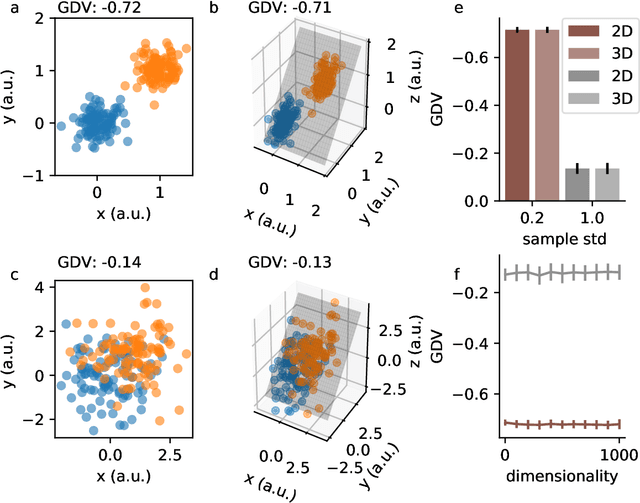
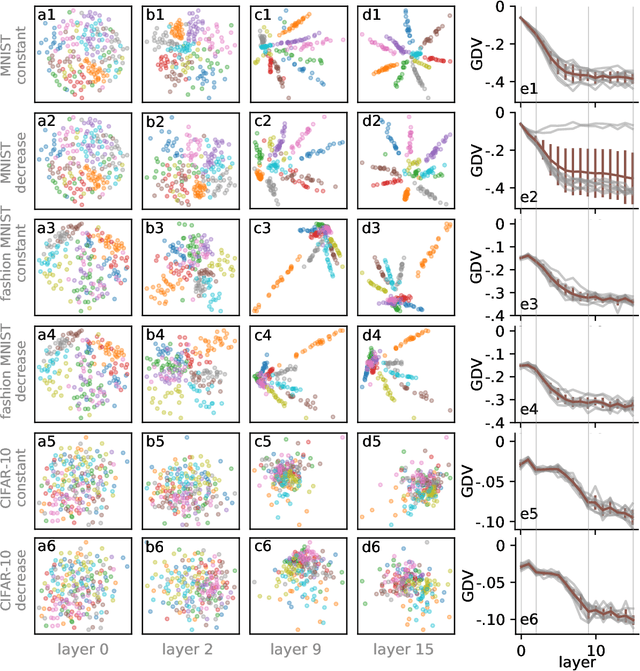
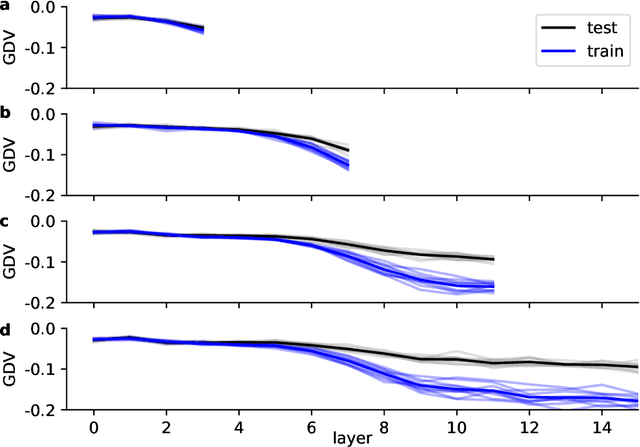
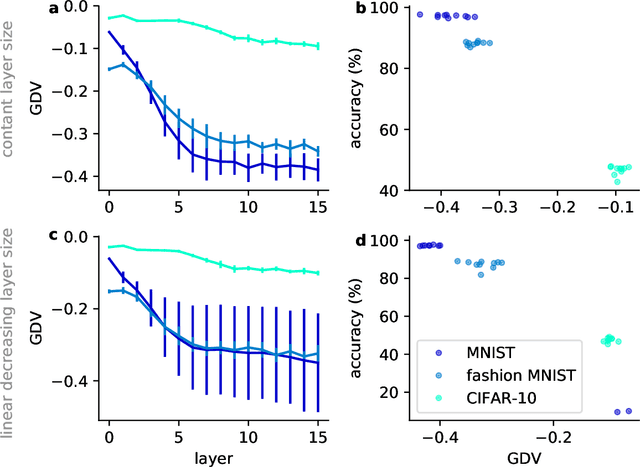
Deep neural networks use stacked layers of feature detectors to repeatedly transform the input data, so that structurally different classes of input become well separated in the final layer. While the method has turned out extremely powerful in many applications, its success depends critically on the correct choice of hyperparameters, in particular the number of network layers. Here, we introduce a new measure, called the generalized discrimination value (GDV), which quantifies how well different object classes separate in each layer. Due to its definition, the GDV is invariant to translation and scaling of the input data, independent of the number of features, as well as independent of the number and permutation of the neurons within a layer. We compute the GDV in each layer of a Deep Belief Network that was trained unsupervised on the MNIST data set. Strikingly, we find that the GDV first improves with each successive network layer, but then gets worse again beyond layer 30, thus indicating the optimal network depth for this data classification task. Our further investigations suggest that the GDV can serve as a universal tool to determine the optimal number of layers in deep neural networks for any type of input data.