Jonas Rietsch
How deep is deep enough? - Optimizing deep neural network architecture
Nov 05, 2018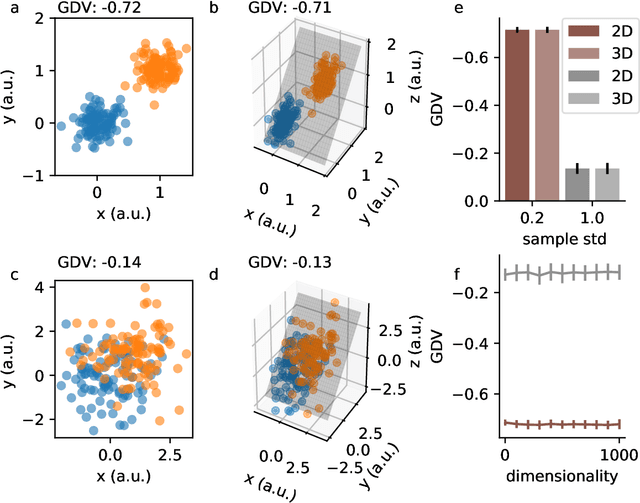
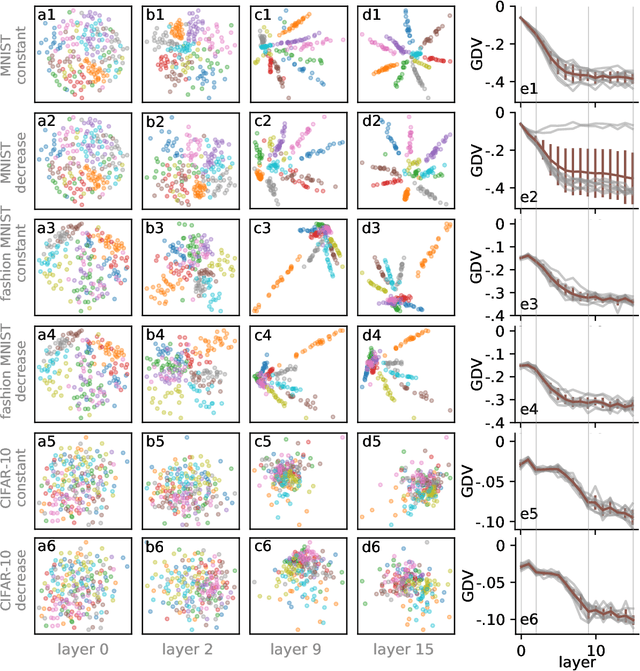
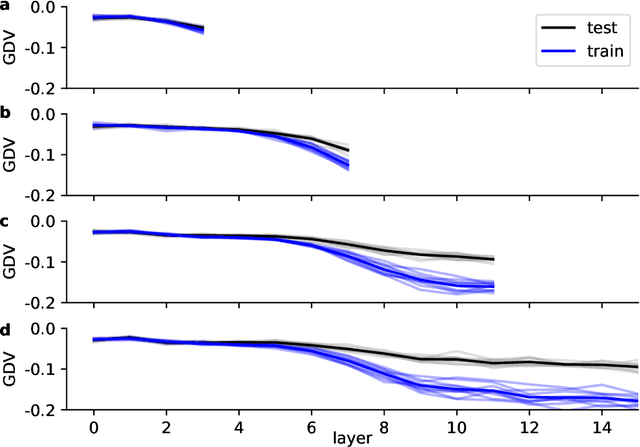
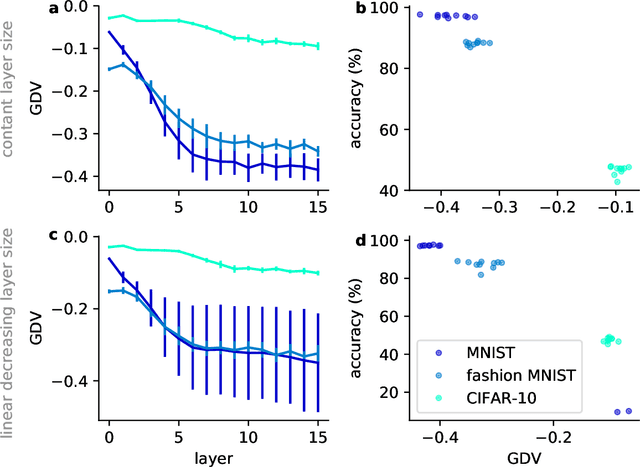
Abstract:Deep neural networks use stacked layers of feature detectors to repeatedly transform the input data, so that structurally different classes of input become well separated in the final layer. While the method has turned out extremely powerful in many applications, its success depends critically on the correct choice of hyperparameters, in particular the number of network layers. Here, we introduce a new measure, called the generalized discrimination value (GDV), which quantifies how well different object classes separate in each layer. Due to its definition, the GDV is invariant to translation and scaling of the input data, independent of the number of features, as well as independent of the number and permutation of the neurons within a layer. We compute the GDV in each layer of a Deep Belief Network that was trained unsupervised on the MNIST data set. Strikingly, we find that the GDV first improves with each successive network layer, but then gets worse again beyond layer 30, thus indicating the optimal network depth for this data classification task. Our further investigations suggest that the GDV can serve as a universal tool to determine the optimal number of layers in deep neural networks for any type of input data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge