Predictive Coding and Stochastic Resonance: Towards a Unified Theory of Auditory (Phantom) Perception

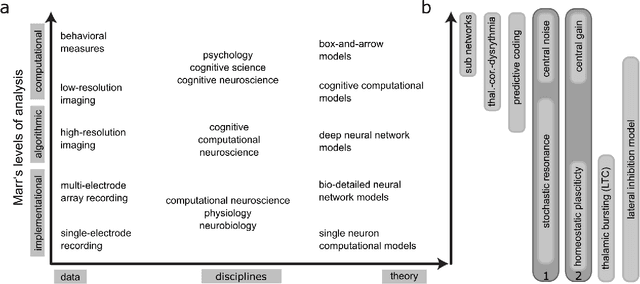
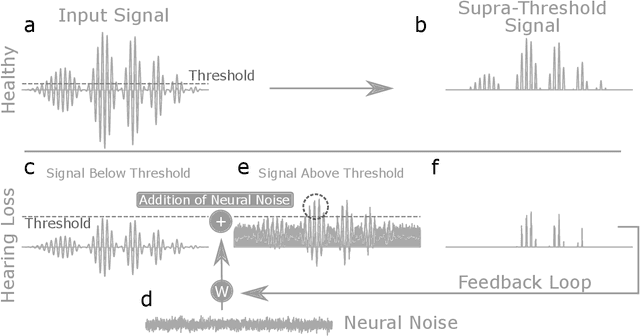
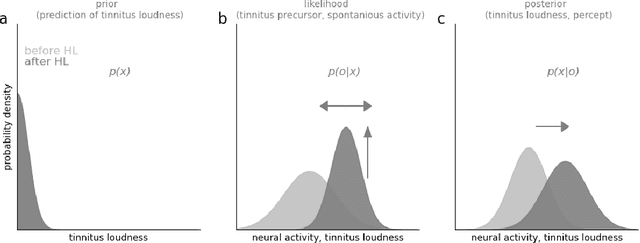
Cognitive computational neuroscience (CCN) suggests that to gain a mechanistic understanding of brain function, hypothesis driven experiments should be accompanied by biologically plausible computational models. This novel research paradigm offers a way from alchemy to chemistry, in auditory neuroscience. With a special focus on tinnitus - as the prime example of auditory phantom perception - we review recent work at the intersection of artificial intelligence, psychology, and neuroscience, foregrounding the idea that experiments will yield mechanistic insight only when employed to test formal or computational models. This view challenges the popular notion that tinnitus research is primarily data limited, and that producing large, multi-modal, and complex data-sets, analyzed with advanced data analysis algorithms, will lead to fundamental insights into how tinnitus emerges. We conclude that two fundamental processing principles - being ubiquitous in the brain - best fit to a vast number of experimental results and therefore provide the most explanatory power: predictive coding as a top-down, and stochastic resonance as a complementary bottom-up mechanism. Furthermore, we argue that even though contemporary artificial intelligence and machine learning approaches largely lack biological plausibility, the models to be constructed will have to draw on concepts from these fields; since they provide a formal account of the requisite computations that underlie brain function. Nevertheless, biological fidelity will have to be addressed, allowing for testing possible treatment strategies in silico, before application in animal or patient studies. This iteration of computational and empirical studies may help to open the "black boxes" of both machine learning and the human brain.

How deep is deep enough? - Optimizing deep neural network architecture

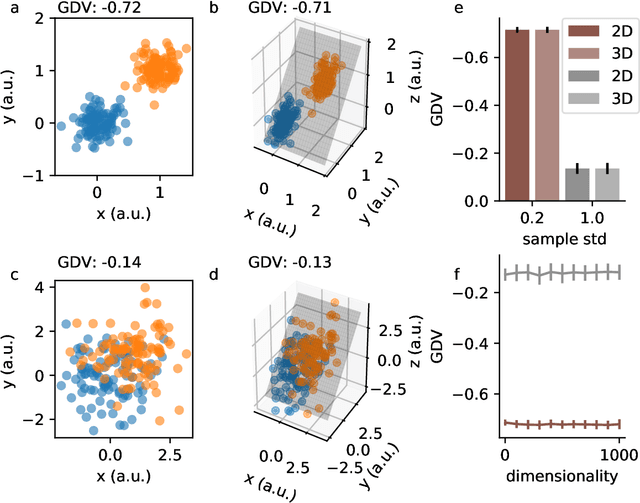
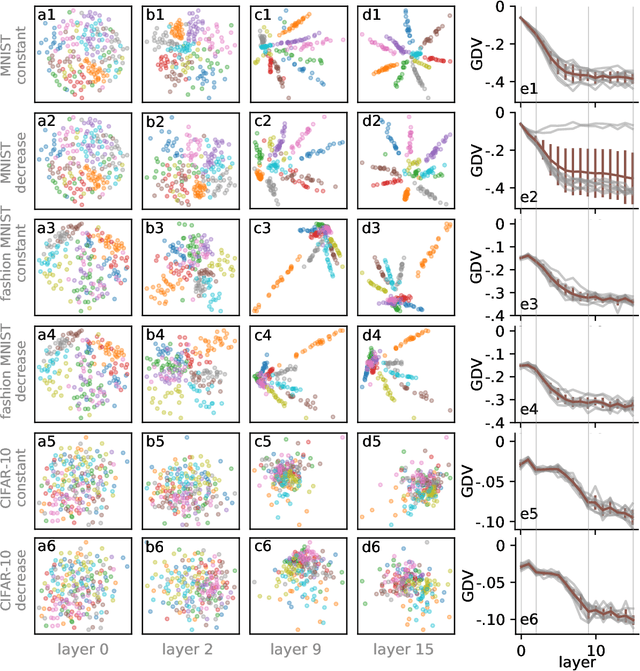
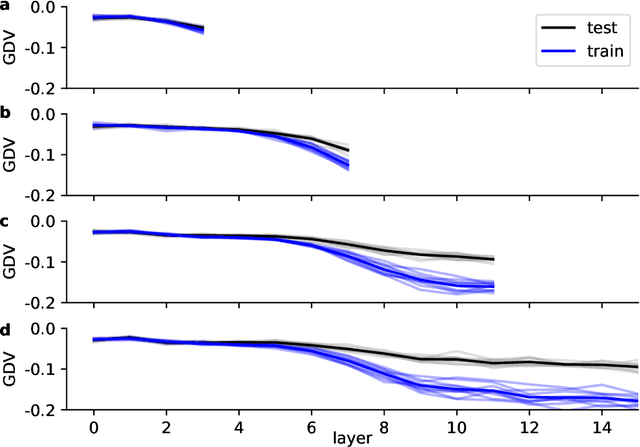
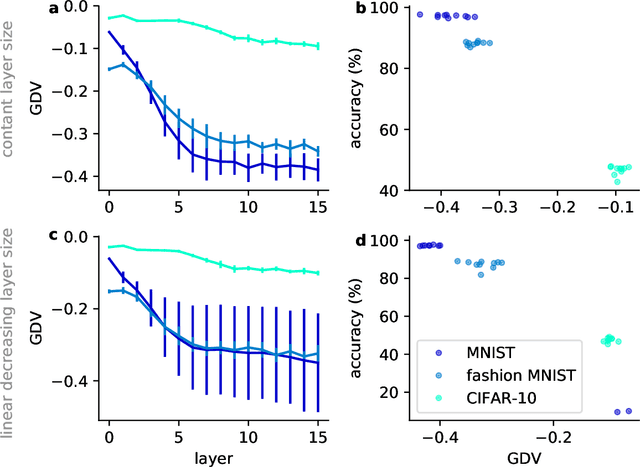
Deep neural networks use stacked layers of feature detectors to repeatedly transform the input data, so that structurally different classes of input become well separated in the final layer. While the method has turned out extremely powerful in many applications, its success depends critically on the correct choice of hyperparameters, in particular the number of network layers. Here, we introduce a new measure, called the generalized discrimination value (GDV), which quantifies how well different object classes separate in each layer. Due to its definition, the GDV is invariant to translation and scaling of the input data, independent of the number of features, as well as independent of the number and permutation of the neurons within a layer. We compute the GDV in each layer of a Deep Belief Network that was trained unsupervised on the MNIST data set. Strikingly, we find that the GDV first improves with each successive network layer, but then gets worse again beyond layer 30, thus indicating the optimal network depth for this data classification task. Our further investigations suggest that the GDV can serve as a universal tool to determine the optimal number of layers in deep neural networks for any type of input data.