Beyond Labels: Advancing Cluster Analysis with the Entropy of Distance Distribution (EDD)
Paper and Code
Nov 28, 2023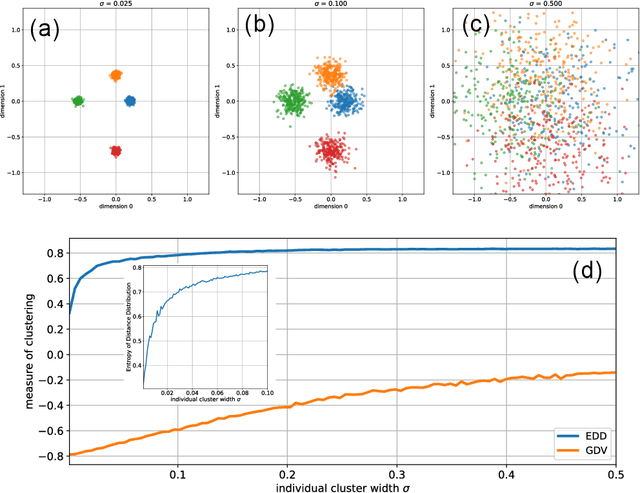

In the evolving landscape of data science, the accurate quantification of clustering in high-dimensional data sets remains a significant challenge, especially in the absence of predefined labels. This paper introduces a novel approach, the Entropy of Distance Distribution (EDD), which represents a paradigm shift in label-free clustering analysis. Traditional methods, reliant on discrete labels, often struggle to discern intricate cluster patterns in unlabeled data. EDD, however, leverages the characteristic differences in pairwise point-to-point distances to discern clustering tendencies, independent of data labeling. Our method employs the Shannon information entropy to quantify the 'peakedness' or 'flatness' of distance distributions in a data set. This entropy measure, normalized against its maximum value, effectively distinguishes between strongly clustered data (indicated by pronounced peaks in distance distribution) and more homogeneous, non-clustered data sets. This label-free quantification is resilient against global translations and permutations of data points, and with an additional dimension-wise z-scoring, it becomes invariant to data set scaling. We demonstrate the efficacy of EDD through a series of experiments involving two-dimensional data spaces with Gaussian cluster centers. Our findings reveal a monotonic increase in the EDD value with the widening of cluster widths, moving from well-separated to overlapping clusters. This behavior underscores the method's sensitivity and accuracy in detecting varying degrees of clustering. EDD's potential extends beyond conventional clustering analysis, offering a robust, scalable tool for unraveling complex data structures without reliance on pre-assigned labels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge