Recursive Least Squares Advantage Actor-Critic Algorithms

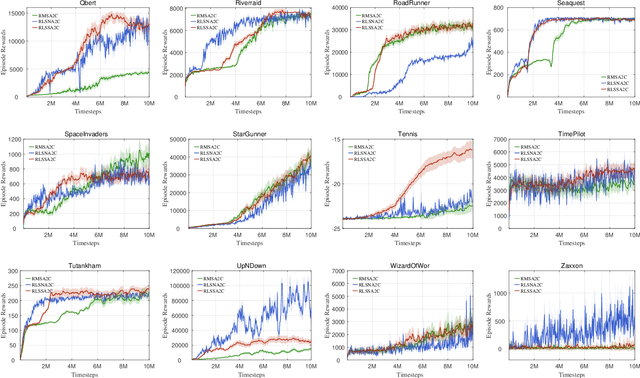
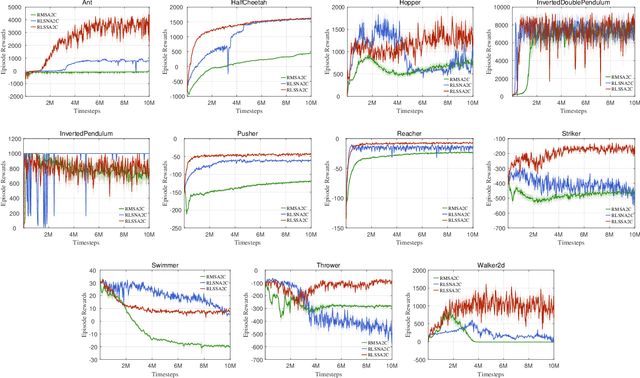
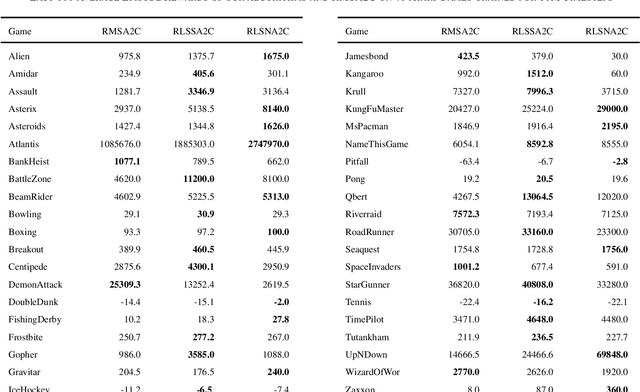
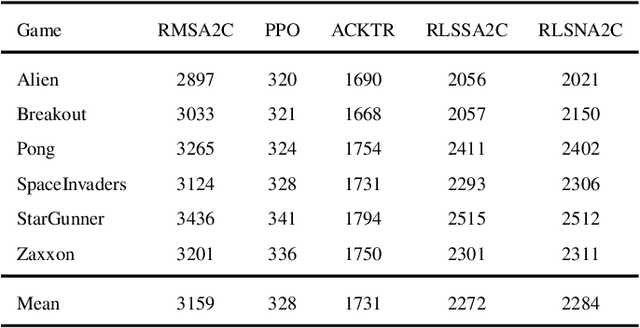
As an important algorithm in deep reinforcement learning, advantage actor critic (A2C) has been widely succeeded in both discrete and continuous control tasks with raw pixel inputs, but its sample efficiency still needs to improve more. In traditional reinforcement learning, actor-critic algorithms generally use the recursive least squares (RLS) technology to update the parameter of linear function approximators for accelerating their convergence speed. However, A2C algorithms seldom use this technology to train deep neural networks (DNNs) for improving their sample efficiency. In this paper, we propose two novel RLS-based A2C algorithms and investigate their performance. Both proposed algorithms, called RLSSA2C and RLSNA2C, use the RLS method to train the critic network and the hidden layers of the actor network. The main difference between them is at the policy learning step. RLSSA2C uses an ordinary first-order gradient descent algorithm and the standard policy gradient to learn the policy parameter. RLSNA2C uses the Kronecker-factored approximation, the RLS method and the natural policy gradient to learn the compatible parameter and the policy parameter. In addition, we analyze the complexity and convergence of both algorithms, and present three tricks for further improving their convergence speed. Finally, we demonstrate the effectiveness of both algorithms on 40 games in the Atari 2600 environment and 11 tasks in the MuJoCo environment. From the experimental results, it is shown that our both algorithms have better sample efficiency than the vanilla A2C on most games or tasks, and have higher computational efficiency than other two state-of-the-art algorithms.

Recursive Least Squares for Training and Pruning Convolutional Neural Networks

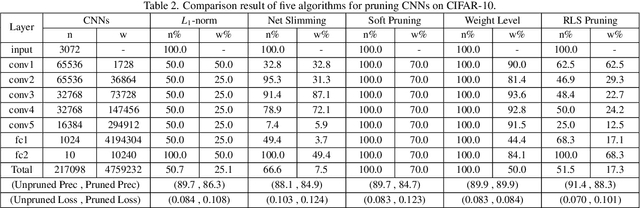
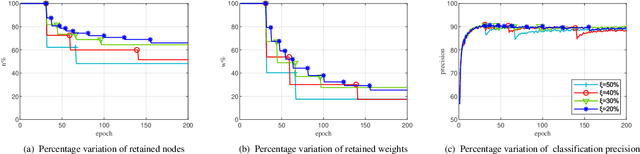
Convolutional neural networks (CNNs) have succeeded in many practical applications. However, their high computation and storage requirements often make them difficult to deploy on resource-constrained devices. In order to tackle this issue, many pruning algorithms have been proposed for CNNs, but most of them can't prune CNNs to a reasonable level. In this paper, we propose a novel algorithm for training and pruning CNNs based on the recursive least squares (RLS) optimization. After training a CNN for some epochs, our algorithm combines inverse input autocorrelation matrices and weight matrices to evaluate and prune unimportant input channels or nodes layer by layer. Then, our algorithm will continue to train the pruned network, and won't do the next pruning until the pruned network recovers the full performance of the old network. Besides for CNNs, the proposed algorithm can be used for feedforward neural networks (FNNs). Three experiments on MNIST, CIFAR-10 and SVHN datasets show that our algorithm can achieve the more reasonable pruning and have higher learning efficiency than other four popular pruning algorithms.

Recursive Least Squares Policy Control with Echo State Network

The echo state network (ESN) is a special type of recurrent neural networks for processing the time-series dataset. However, limited by the strong correlation among sequential samples of the agent, ESN-based policy control algorithms are difficult to use the recursive least squares (RLS) algorithm to update the ESN's parameters. To solve this problem, we propose two novel policy control algorithms, ESNRLS-Q and ESNRLS-Sarsa. Firstly, to reduce the correlation of training samples, we use the leaky integrator ESN and the mini-batch learning mode. Secondly, to make RLS suitable for training ESN in mini-batch mode, we present a new mean-approximation method for updating the RLS correlation matrix. Thirdly, to prevent ESN from over-fitting, we use the L1 regularization technique. Lastly, to prevent the target state-action value from overestimation, we employ the Mellowmax method. Simulation results show that our algorithms have good convergence performance.

Revisiting Recursive Least Squares for Training Deep Neural Networks

Recursive least squares (RLS) algorithms were once widely used for training small-scale neural networks, due to their fast convergence. However, previous RLS algorithms are unsuitable for training deep neural networks (DNNs), since they have high computational complexity and too many preconditions. In this paper, to overcome these drawbacks, we propose three novel RLS optimization algorithms for training feedforward neural networks, convolutional neural networks and recurrent neural networks (including long short-term memory networks), by using the error backpropagation and our average-approximation RLS method, together with the equivalent gradients of the linear least squares loss function with respect to the linear outputs of hidden layers. Compared with previous RLS optimization algorithms, our algorithms are simple and elegant. They can be viewed as an improved stochastic gradient descent (SGD) algorithm, which uses the inverse autocorrelation matrix of each layer as the adaptive learning rate. Their time and space complexities are only several times those of SGD. They only require the loss function to be the mean squared error and the activation function of the output layer to be invertible. In fact, our algorithms can be also used in combination with other first-order optimization algorithms without requiring these two preconditions. In addition, we present two improved methods for our algorithms. Finally, we demonstrate their effectiveness compared to the Adam algorithm on MNIST, CIFAR-10 and IMDB datasets, and investigate the influences of their hyperparameters experimentally.

A Computational Model of the Short-Cut Rule for 2D Shape Decomposition

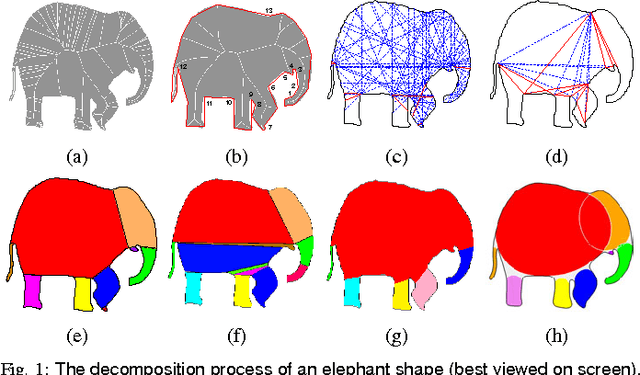
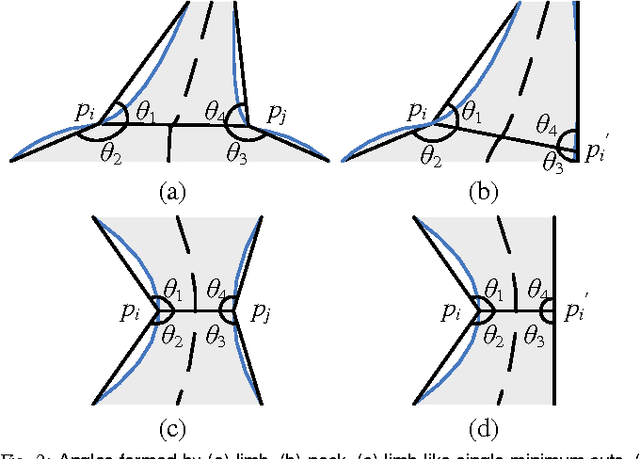
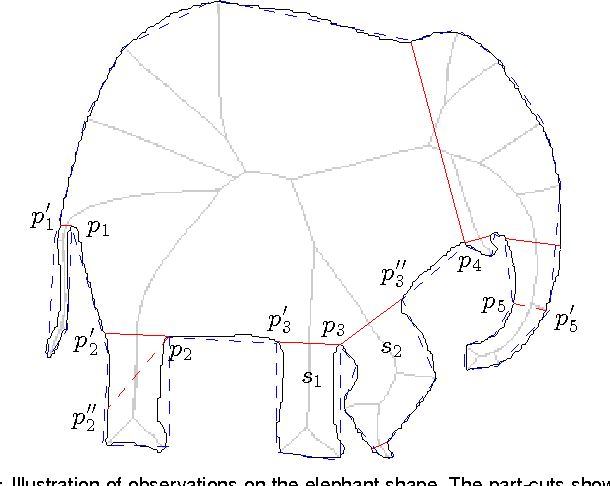
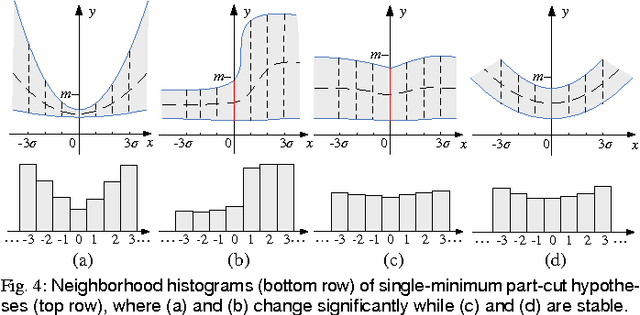
We propose a new 2D shape decomposition method based on the short-cut rule. The short-cut rule originates from cognition research, and states that the human visual system prefers to partition an object into parts using the shortest possible cuts. We propose and implement a computational model for the short-cut rule and apply it to the problem of shape decomposition. The model we proposed generates a set of cut hypotheses passing through the points on the silhouette which represent the negative minima of curvature. We then show that most part-cut hypotheses can be eliminated by analysis of local properties of each. Finally, the remaining hypotheses are evaluated in ascending length order, which guarantees that of any pair of conflicting cuts only the shortest will be accepted. We demonstrate that, compared with state-of-the-art shape decomposition methods, the proposed approach achieves decomposition results which better correspond to human intuition as revealed in psychological experiments.