NeuroLifting: Neural Inference on Markov Random Fields at Scale

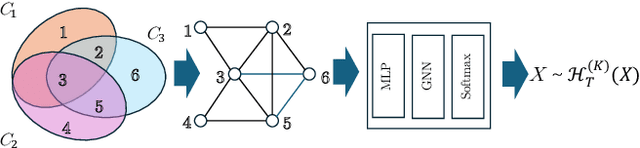
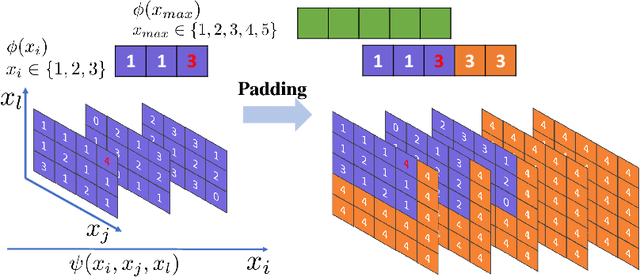
Inference in large-scale Markov Random Fields (MRFs) is a critical yet challenging task, traditionally approached through approximate methods like belief propagation and mean field, or exact methods such as the Toulbar2 solver. These strategies often fail to strike an optimal balance between efficiency and solution quality, particularly as the problem scale increases. This paper introduces NeuroLifting, a novel technique that leverages Graph Neural Networks (GNNs) to reparameterize decision variables in MRFs, facilitating the use of standard gradient descent optimization. By extending traditional lifting techniques into a non-parametric neural network framework, NeuroLifting benefits from the smooth loss landscape of neural networks, enabling efficient and parallelizable optimization. Empirical results demonstrate that, on moderate scales, NeuroLifting performs very close to the exact solver Toulbar2 in terms of solution quality, significantly surpassing existing approximate methods. Notably, on large-scale MRFs, NeuroLifting delivers superior solution quality against all baselines, as well as exhibiting linear computational complexity growth. This work presents a significant advancement in MRF inference, offering a scalable and effective solution for large-scale problems.

Rethinking the "Heatmap + Monte Carlo Tree Search" Paradigm for Solving Large Scale TSP

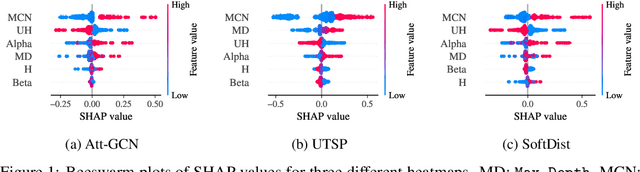
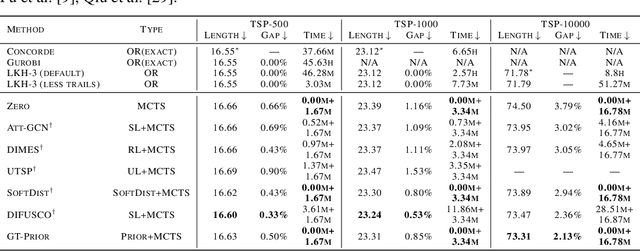
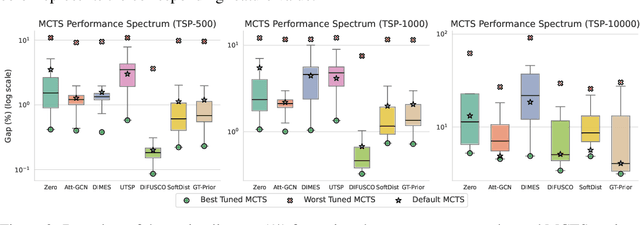
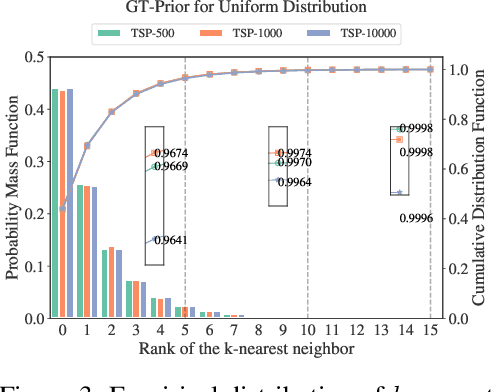
The Travelling Salesman Problem (TSP) remains a fundamental challenge in combinatorial optimization, inspiring diverse algorithmic strategies. This paper revisits the "heatmap + Monte Carlo Tree Search (MCTS)" paradigm that has recently gained traction for learning-based TSP solutions. Within this framework, heatmaps encode the likelihood of edges forming part of the optimal tour, and MCTS refines this probabilistic guidance to discover optimal solutions. Contemporary approaches have predominantly emphasized the refinement of heatmap generation through sophisticated learning models, inadvertently sidelining the critical role of MCTS. Our extensive empirical analysis reveals two pivotal insights: 1) The configuration of MCTS strategies profoundly influences the solution quality, demanding meticulous tuning to leverage their full potential; 2) Our findings demonstrate that a rudimentary and parameter-free heatmap, derived from the intrinsic $k$-nearest nature of TSP, can rival or even surpass the performance of complicated heatmaps, with strong generalizability across various scales. Empirical evaluations across various TSP scales underscore the efficacy of our approach, achieving competitive results. These observations challenge the prevailing focus on heatmap sophistication, advocating a reevaluation of the paradigm to harness both components synergistically. Our code is available at: https://github.com/LOGO-CUHKSZ/rethink_mcts_tsp.

Enhancing Graph Self-Supervised Learning with Graph Interplay

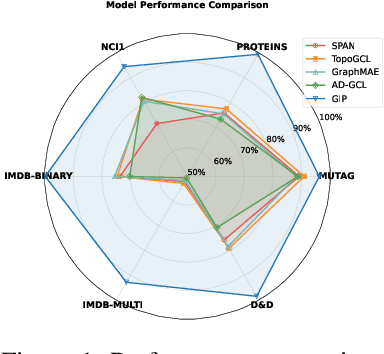
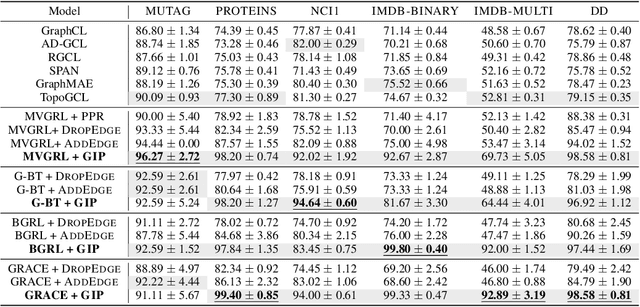
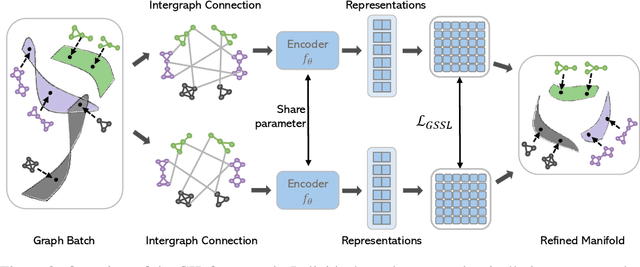
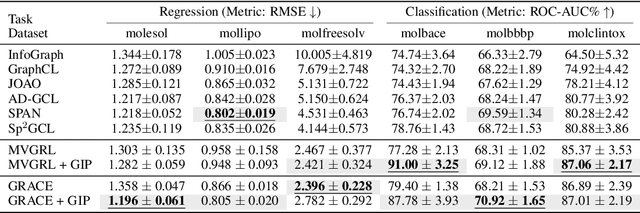
Graph self-supervised learning (GSSL) has emerged as a compelling framework for extracting informative representations from graph-structured data without extensive reliance on labeled inputs. In this study, we introduce Graph Interplay (GIP), an innovative and versatile approach that significantly enhances the performance equipped with various existing GSSL methods. To this end, GIP advocates direct graph-level communications by introducing random inter-graph edges within standard batches. Against GIP's simplicity, we further theoretically show that \textsc{GIP} essentially performs a principled manifold separation via combining inter-graph message passing and GSSL, bringing about more structured embedding manifolds and thus benefits a series of downstream tasks. Our empirical study demonstrates that GIP surpasses the performance of prevailing GSSL methods across multiple benchmarks by significant margins, highlighting its potential as a breakthrough approach. Besides, GIP can be readily integrated into a series of GSSL methods and consistently offers additional performance gain. This advancement not only amplifies the capability of GSSL but also potentially sets the stage for a novel graph learning paradigm in a broader sense.

Do spectral cues matter in contrast-based graph self-supervised learning?

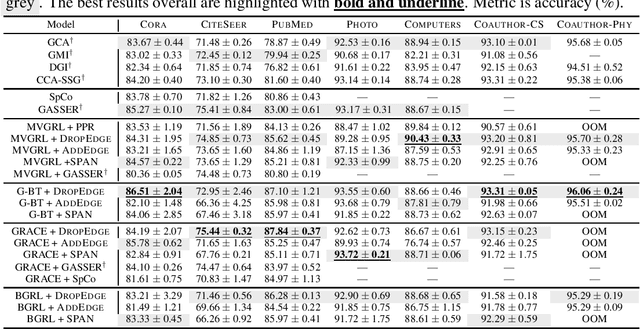
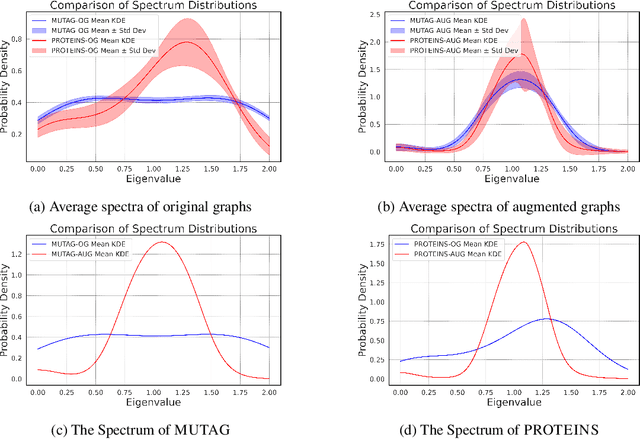
The recent surge in contrast-based graph self-supervised learning has prominently featured an intensified exploration of spectral cues. However, an intriguing paradox emerges, as methods grounded in seemingly conflicting assumptions or heuristic approaches regarding the spectral domain demonstrate notable enhancements in learning performance. This paradox prompts a critical inquiry into the genuine contribution of spectral information to contrast-based graph self-supervised learning. This study undertakes an extensive investigation into this inquiry, conducting a thorough study of the relationship between spectral characteristics and the learning outcomes of contemporary methodologies. Based on this analysis, we claim that the effectiveness and significance of spectral information need to be questioned. Instead, we revisit simple edge perturbation: random edge dropping designed for node-level self-supervised learning and random edge adding intended for graph-level self-supervised learning. Compelling evidence is presented that these simple yet effective strategies consistently yield superior performance while demanding significantly fewer computational resources compared to all prior spectral augmentation methods. The proposed insights represent a significant leap forward in the field, potentially reshaping the understanding and implementation of graph self-supervised learning.

Graph Learning with Distributional Edge Layouts

Graph Neural Networks (GNNs) learn from graph-structured data by passing local messages between neighboring nodes along edges on certain topological layouts. Typically, these topological layouts in modern GNNs are deterministically computed (e.g., attention-based GNNs) or locally sampled (e.g., GraphSage) under heuristic assumptions. In this paper, we for the first time pose that these layouts can be globally sampled via Langevin dynamics following Boltzmann distribution equipped with explicit physical energy, leading to higher feasibility in the physical world. We argue that such a collection of sampled/optimized layouts can capture the wide energy distribution and bring extra expressivity on top of WL-test, therefore easing downstream tasks. As such, we propose Distributional Edge Layouts (DELs) to serve as a complement to a variety of GNNs. DEL is a pre-processing strategy independent of subsequent GNN variants, thus being highly flexible. Experimental results demonstrate that DELs consistently and substantially improve a series of GNN baselines, achieving state-of-the-art performance on multiple datasets.

Boosting Graph Pooling with Persistent Homology

Recently, there has been an emerging trend to integrate persistent homology (PH) into graph neural networks (GNNs) to enrich expressive power. However, naively plugging PH features into GNN layers always results in marginal improvement with low interpretability. In this paper, we investigate a novel mechanism for injecting global topological invariance into pooling layers using PH, motivated by the observation that filtration operation in PH naturally aligns graph pooling in a cut-off manner. In this fashion, message passing in the coarsened graph acts along persistent pooled topology, leading to improved performance. Experimentally, we apply our mechanism to a collection of graph pooling methods and observe consistent and substantial performance gain over several popular datasets, demonstrating its wide applicability and flexibility.

Molecular Conformation Generation via Shifting Scores

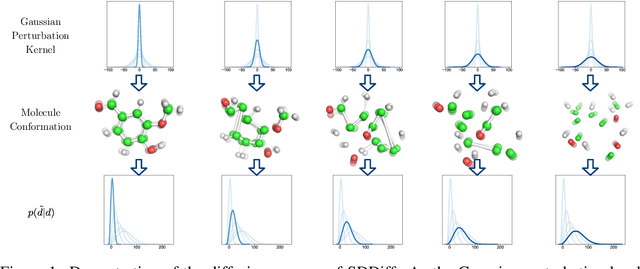
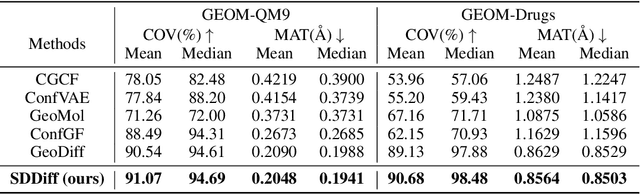
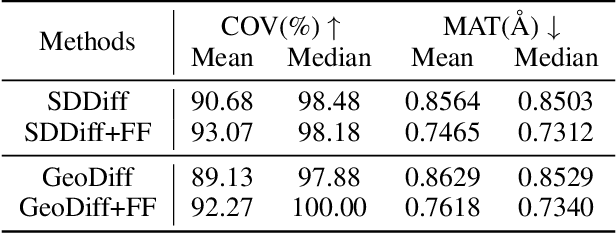
Molecular conformation generation, a critical aspect of computational chemistry, involves producing the three-dimensional conformer geometry for a given molecule. Generating molecular conformation via diffusion requires learning to reverse a noising process. Diffusion on inter-atomic distances instead of conformation preserves SE(3)-equivalence and shows superior performance compared to alternative techniques, whereas related generative modelings are predominantly based upon heuristical assumptions. In response to this, we propose a novel molecular conformation generation approach driven by the observation that the disintegration of a molecule can be viewed as casting increasing force fields to its composing atoms, such that the distribution of the change of inter-atomic distance shifts from Gaussian to Maxwell-Boltzmann distribution. The corresponding generative modeling ensures a feasible inter-atomic distance geometry and exhibits time reversibility. Experimental results on molecular datasets demonstrate the advantages of the proposed shifting distribution compared to the state-of-the-art.