Neural Graduated Assignment for Maximum Common Edge Subgraphs

The Maximum Common Edge Subgraph (MCES) problem is a crucial challenge with significant implications in domains such as biology and chemistry. Traditional approaches, which include transformations into max-clique and search-based algorithms, suffer from scalability issues when dealing with larger instances. This paper introduces ``Neural Graduated Assignment'' (NGA), a simple, scalable, unsupervised-training-based method that addresses these limitations by drawing inspiration from the classical Graduated Assignment (GA) technique. Central to NGA is stacking of neural components that closely resemble the GA process, but with the reparameterization of learnable temperature into higher dimension. We further theoretically analyze the learning dynamics of NGA, showing its design leads to fast convergence, better exploration-exploitation tradeoff, and ability to escape local optima. Extensive experiments across MCES computation, graph similarity estimation, and graph retrieval tasks reveal that NGA not only significantly improves computation time and scalability on large instances but also enhances performance compared to existing methodologies. The introduction of NGA marks a significant advancement in the computation of MCES and offers insights into other assignment problems.

NeuroLifting: Neural Inference on Markov Random Fields at Scale

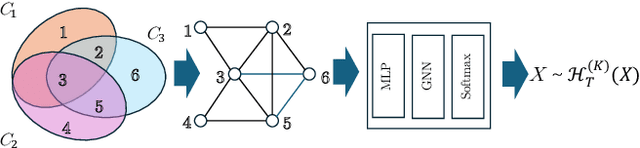
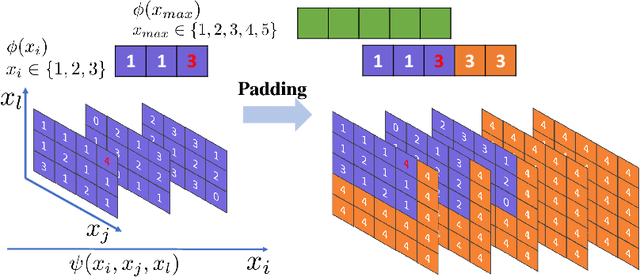
Inference in large-scale Markov Random Fields (MRFs) is a critical yet challenging task, traditionally approached through approximate methods like belief propagation and mean field, or exact methods such as the Toulbar2 solver. These strategies often fail to strike an optimal balance between efficiency and solution quality, particularly as the problem scale increases. This paper introduces NeuroLifting, a novel technique that leverages Graph Neural Networks (GNNs) to reparameterize decision variables in MRFs, facilitating the use of standard gradient descent optimization. By extending traditional lifting techniques into a non-parametric neural network framework, NeuroLifting benefits from the smooth loss landscape of neural networks, enabling efficient and parallelizable optimization. Empirical results demonstrate that, on moderate scales, NeuroLifting performs very close to the exact solver Toulbar2 in terms of solution quality, significantly surpassing existing approximate methods. Notably, on large-scale MRFs, NeuroLifting delivers superior solution quality against all baselines, as well as exhibiting linear computational complexity growth. This work presents a significant advancement in MRF inference, offering a scalable and effective solution for large-scale problems.