A sparse coding approach to inverse problems with application to microwave tomography imaging

Inverse imaging problems that are ill-posed can be encountered across multiple domains of science and technology, ranging from medical diagnosis to astronomical studies. To reconstruct images from incomplete and distorted data, it is necessary to create algorithms that can take into account both, the physical mechanisms responsible for generating these measurements and the intrinsic characteristics of the images being analyzed. In this work, the sparse representation of images is reviewed, which is a realistic, compact and effective generative model for natural images inspired by the visual system of mammals. It enables us to address ill-posed linear inverse problems by training the model on a vast collection of images. Moreover, we extend the application of sparse coding to solve the non-linear and ill-posed problem in microwave tomography imaging, which could lead to a significant improvement of the state-of-the-arts algorithms.

Serial-EMD: Fast Empirical Mode Decomposition Method for Multi-dimensional Signals Based on Serialization

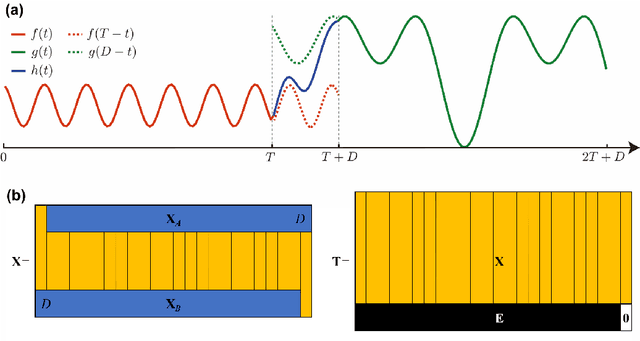
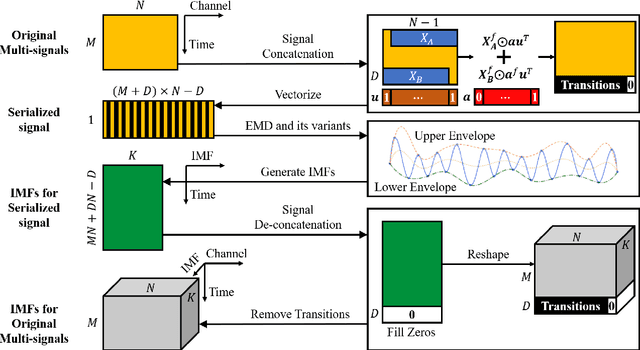
Empirical mode decomposition (EMD) has developed into a prominent tool for adaptive, scale-based signal analysis in various fields like robotics, security and biomedical engineering. Since the dramatic increase in amount of data puts forward higher requirements for the capability of real-time signal analysis, it is difficult for existing EMD and its variants to trade off the growth of data dimension and the speed of signal analysis. In order to decompose multi-dimensional signals at a faster speed, we present a novel signal-serialization method (serial-EMD), which concatenates multi-variate or multi-dimensional signals into a one-dimensional signal and uses various one-dimensional EMD algorithms to decompose it. To verify the effects of the proposed method, synthetic multi-variate time series, artificial 2D images with various textures and real-world facial images are tested. Compared with existing multi-EMD algorithms, the decomposition time becomes significantly reduced. In addition, the results of facial recognition with Intrinsic Mode Functions (IMFs) extracted using our method can achieve a higher accuracy than those obtained by existing multi-EMD algorithms, which demonstrates the superior performance of our method in terms of the quality of IMFs. Furthermore, this method can provide a new perspective to optimize the existing EMD algorithms, that is, transforming the structure of the input signal rather than being constrained by developing envelope computation techniques or signal decomposition methods. In summary, the study suggests that the serial-EMD technique is a highly competitive and fast alternative for multi-dimensional signal analysis.

Learning from Incomplete Data by Simultaneous Training of Neural Networks and Sparse Coding

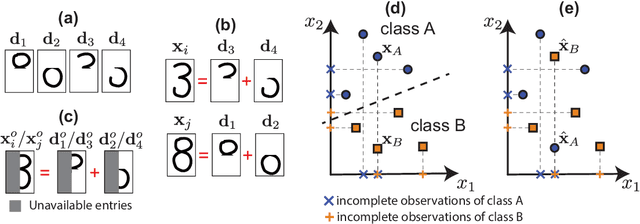
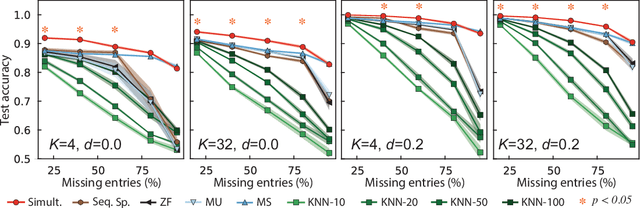
Handling correctly incomplete datasets in machine learning is a fundamental and classical challenge. In this paper, the problem of training a classifier on a dataset with missing features, and its application to a complete or incomplete test dataset, is addressed. A supervised learning method is developed to train a general classifier, such as a logistic regression or a deep neural network, using only a limited number of features per sample, while assuming sparse representations of data vectors on an unknown dictionary. The pattern of missing features is allowed to be different for each input data instance and can be either random or structured. The proposed method simultaneously learns the classifier, the dictionary and the corresponding sparse representation of each input data sample. A theoretical analysis is provided, comparing this method with the standard imputation approach, which consists of performing data completion followed by training the classifier with those reconstructions. Sufficient conditions are identified such that, if it is possible to train a classifier on incomplete observations so that their reconstructions are well separated by a hyperplane, then the same classifier also correctly separates the original (unobserved) data samples. Extensive simulation results on synthetic and well-known reference datasets are presented that validate our theoretical findings and demonstrate the effectiveness of the proposed method compared to traditional data imputation approaches and one state of the art algorithm.

Brain-Computer Interface with Corrupted EEG Data: A Tensor Completion Approach

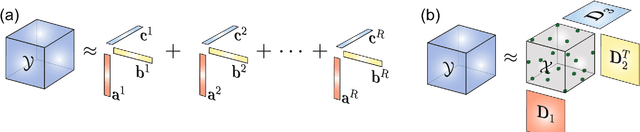
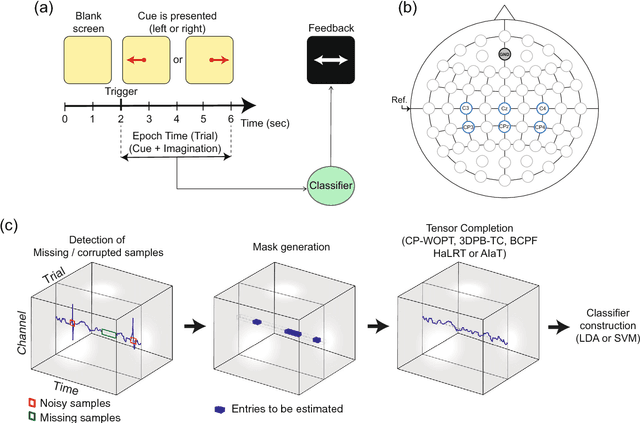
One of the current issues in Brain-Computer Interface is how to deal with noisy Electroencephalography measurements organized as multidimensional datasets. On the other hand, recently, significant advances have been made in multidimensional signal completion algorithms that exploit tensor decomposition models to capture the intricate relationship among entries in a multidimensional signal. We propose to use tensor completion applied to EEG data for improving the classification performance in a motor imagery BCI system with corrupted measurements. Noisy measurements are considered as unknowns that are inferred from a tensor decomposition model. We evaluate the performance of four recently proposed tensor completion algorithms plus a simple interpolation strategy, first with random missing entries and then with missing samples constrained to have a specific structure (random missing channels), which is a more realistic assumption in BCI Applications. We measured the ability of these algorithms to reconstruct the tensor from observed data. Then, we tested the classification accuracy of imagined movement in a BCI experiment with missing samples. We show that for random missing entries, all tensor completion algorithms can recover missing samples increasing the classification performance compared to a simple interpolation approach. For the random missing channels case, we show that tensor completion algorithms help to reconstruct missing channels, significantly improving the accuracy in the classification of motor imagery, however, not at the same level as clean data. Tensor completion algorithms are useful in real BCI applications. The proposed strategy could allow using motor imagery BCI systems even when EEG data is highly affected by missing channels and/or samples, avoiding the need of new acquisitions in the calibration stage.

Higher-Order Partial Least Squares (HOPLS): A Generalized Multi-Linear Regression Method

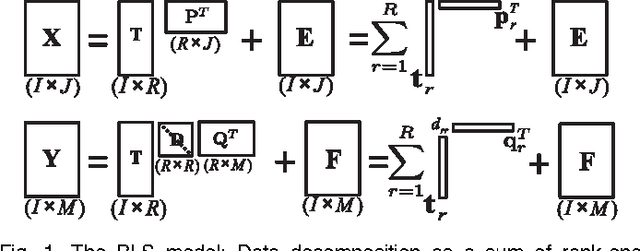
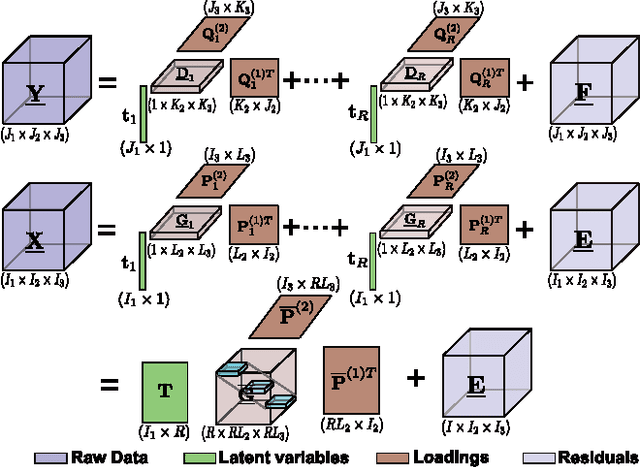
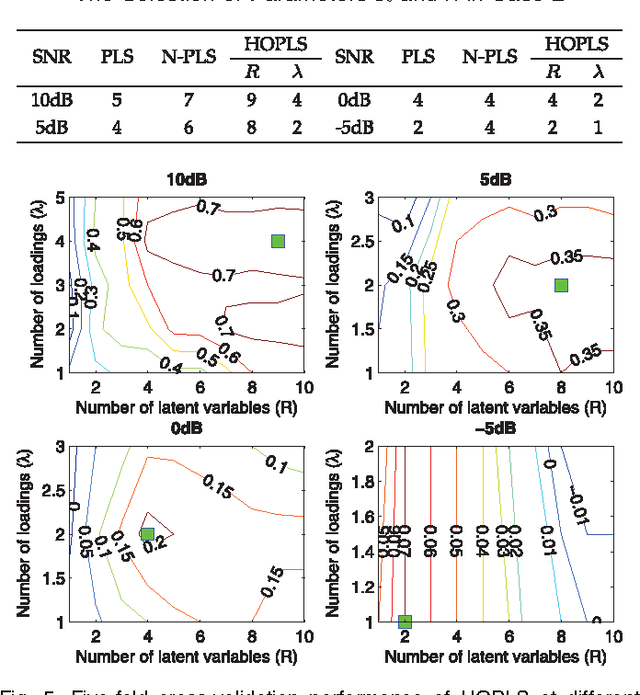
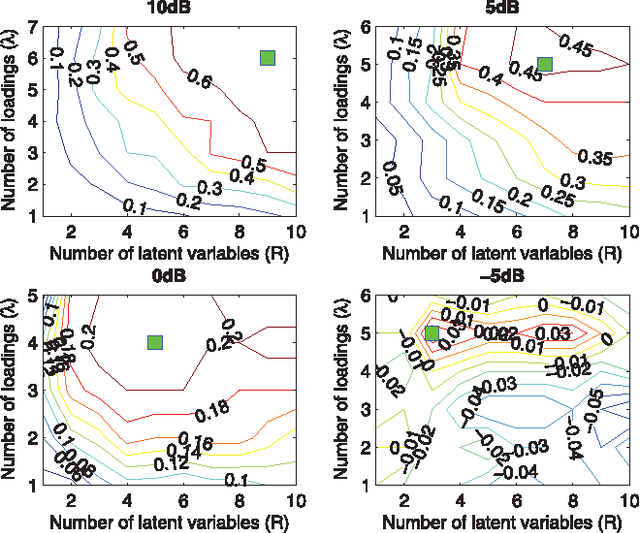
A new generalized multilinear regression model, termed the Higher-Order Partial Least Squares (HOPLS), is introduced with the aim to predict a tensor (multiway array) $\tensor{Y}$ from a tensor $\tensor{X}$ through projecting the data onto the latent space and performing regression on the corresponding latent variables. HOPLS differs substantially from other regression models in that it explains the data by a sum of orthogonal Tucker tensors, while the number of orthogonal loadings serves as a parameter to control model complexity and prevent overfitting. The low dimensional latent space is optimized sequentially via a deflation operation, yielding the best joint subspace approximation for both $\tensor{X}$ and $\tensor{Y}$. Instead of decomposing $\tensor{X}$ and $\tensor{Y}$ individually, higher order singular value decomposition on a newly defined generalized cross-covariance tensor is employed to optimize the orthogonal loadings. A systematic comparison on both synthetic data and real-world decoding of 3D movement trajectories from electrocorticogram (ECoG) signals demonstrate the advantages of HOPLS over the existing methods in terms of better predictive ability, suitability to handle small sample sizes, and robustness to noise.