Higher-Order Partial Least Squares (HOPLS): A Generalized Multi-Linear Regression Method
Paper and Code
Jul 05, 2012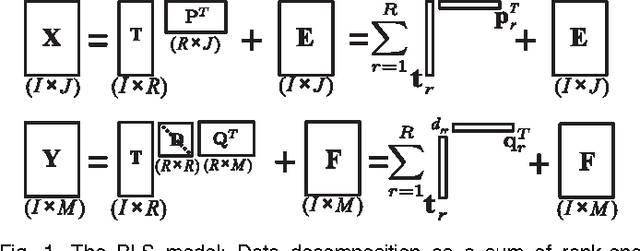
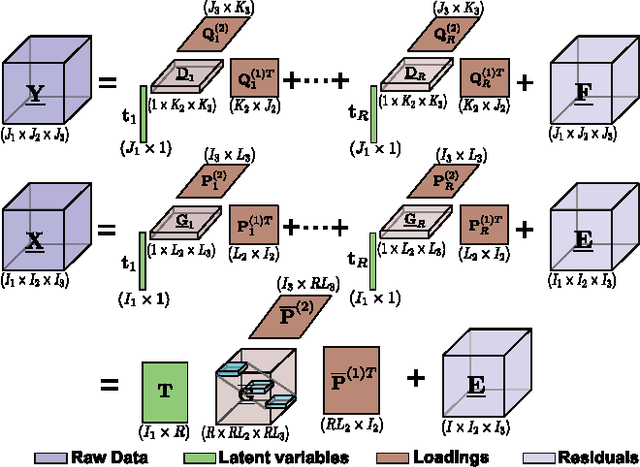
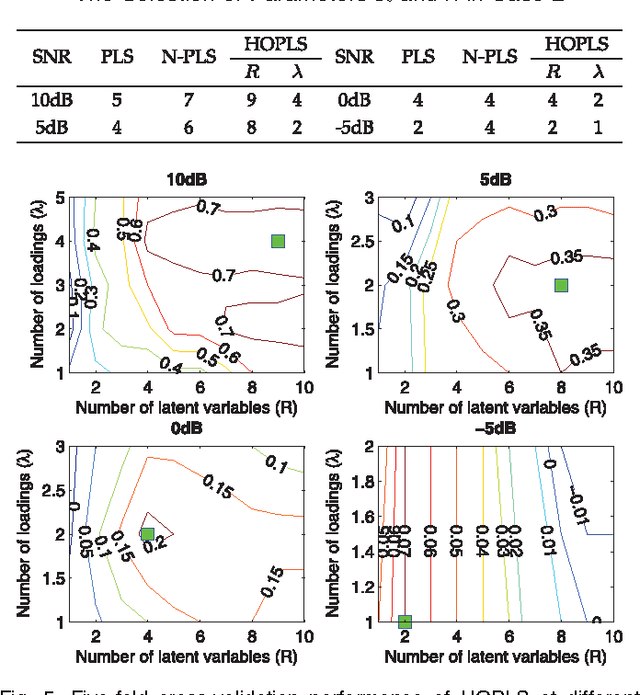
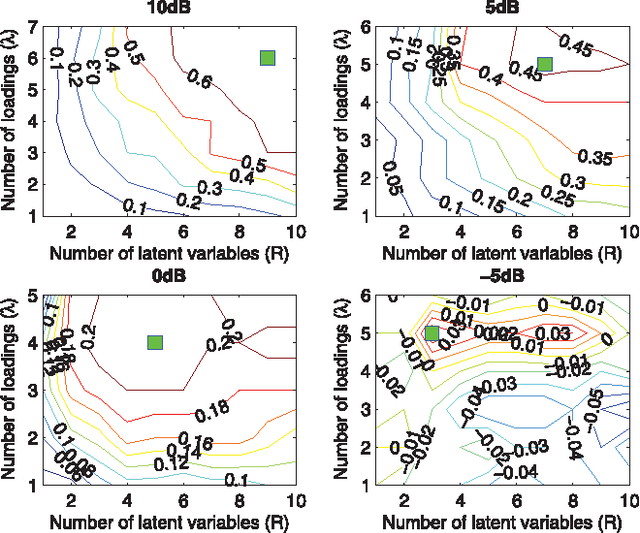
A new generalized multilinear regression model, termed the Higher-Order Partial Least Squares (HOPLS), is introduced with the aim to predict a tensor (multiway array) $\tensor{Y}$ from a tensor $\tensor{X}$ through projecting the data onto the latent space and performing regression on the corresponding latent variables. HOPLS differs substantially from other regression models in that it explains the data by a sum of orthogonal Tucker tensors, while the number of orthogonal loadings serves as a parameter to control model complexity and prevent overfitting. The low dimensional latent space is optimized sequentially via a deflation operation, yielding the best joint subspace approximation for both $\tensor{X}$ and $\tensor{Y}$. Instead of decomposing $\tensor{X}$ and $\tensor{Y}$ individually, higher order singular value decomposition on a newly defined generalized cross-covariance tensor is employed to optimize the orthogonal loadings. A systematic comparison on both synthetic data and real-world decoding of 3D movement trajectories from electrocorticogram (ECoG) signals demonstrate the advantages of HOPLS over the existing methods in terms of better predictive ability, suitability to handle small sample sizes, and robustness to noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge