Adrzej Cichocki
Brain-Computer Interface with Corrupted EEG Data: A Tensor Completion Approach
Jul 26, 2018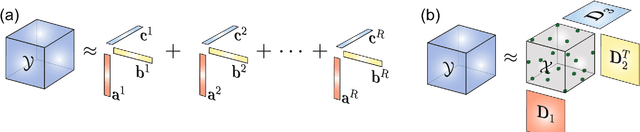


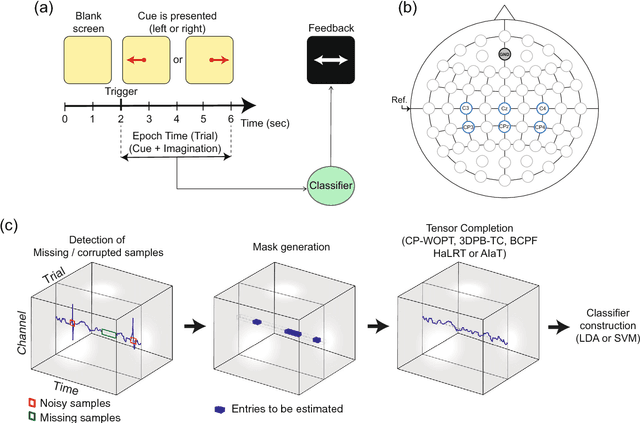
Abstract:One of the current issues in Brain-Computer Interface is how to deal with noisy Electroencephalography measurements organized as multidimensional datasets. On the other hand, recently, significant advances have been made in multidimensional signal completion algorithms that exploit tensor decomposition models to capture the intricate relationship among entries in a multidimensional signal. We propose to use tensor completion applied to EEG data for improving the classification performance in a motor imagery BCI system with corrupted measurements. Noisy measurements are considered as unknowns that are inferred from a tensor decomposition model. We evaluate the performance of four recently proposed tensor completion algorithms plus a simple interpolation strategy, first with random missing entries and then with missing samples constrained to have a specific structure (random missing channels), which is a more realistic assumption in BCI Applications. We measured the ability of these algorithms to reconstruct the tensor from observed data. Then, we tested the classification accuracy of imagined movement in a BCI experiment with missing samples. We show that for random missing entries, all tensor completion algorithms can recover missing samples increasing the classification performance compared to a simple interpolation approach. For the random missing channels case, we show that tensor completion algorithms help to reconstruct missing channels, significantly improving the accuracy in the classification of motor imagery, however, not at the same level as clean data. Tensor completion algorithms are useful in real BCI applications. The proposed strategy could allow using motor imagery BCI systems even when EEG data is highly affected by missing channels and/or samples, avoiding the need of new acquisitions in the calibration stage.
* 21 pages, 3 tables, 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge