PAFUSE: Part-based Diffusion for 3D Whole-Body Pose Estimation

We introduce a novel approach for 3D whole-body pose estimation, addressing the challenge of scale- and deformability- variance across body parts brought by the challenge of extending the 17 major joints on the human body to fine-grained keypoints on the face and hands. In addition to addressing the challenge of exploiting motion in unevenly sampled data, we combine stable diffusion to a hierarchical part representation which predicts the relative locations of fine-grained keypoints within each part (e.g., face) with respect to the part's local reference frame. On the H3WB dataset, our method greatly outperforms the current state of the art, which fails to exploit the temporal information. We also show considerable improvements compared to other spatiotemporal 3D human-pose estimation approaches that fail to account for the body part specificities. Code is available at https://github.com/valeoai/PAFUSE.

Winner-takes-all learners are geometry-aware conditional density estimators

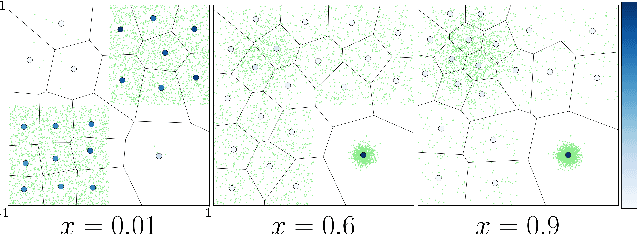
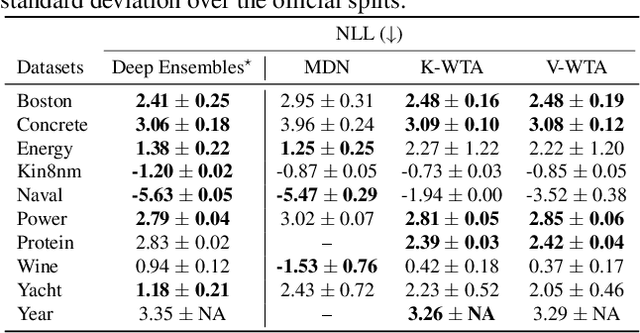
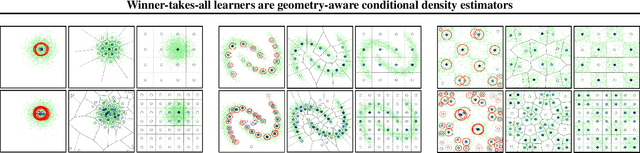
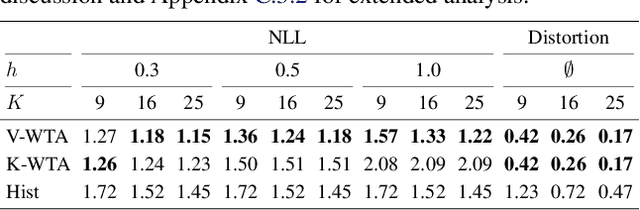
Winner-takes-all training is a simple learning paradigm, which handles ambiguous tasks by predicting a set of plausible hypotheses. Recently, a connection was established between Winner-takes-all training and centroidal Voronoi tessellations, showing that, once trained, hypotheses should quantize optimally the shape of the conditional distribution to predict. However, the best use of these hypotheses for uncertainty quantification is still an open question.In this work, we show how to leverage the appealing geometric properties of the Winner-takes-all learners for conditional density estimation, without modifying its original training scheme. We theoretically establish the advantages of our novel estimator both in terms of quantization and density estimation, and we demonstrate its competitiveness on synthetic and real-world datasets, including audio data.

ManiPose: Manifold-Constrained Multi-Hypothesis 3D Human Pose Estimation

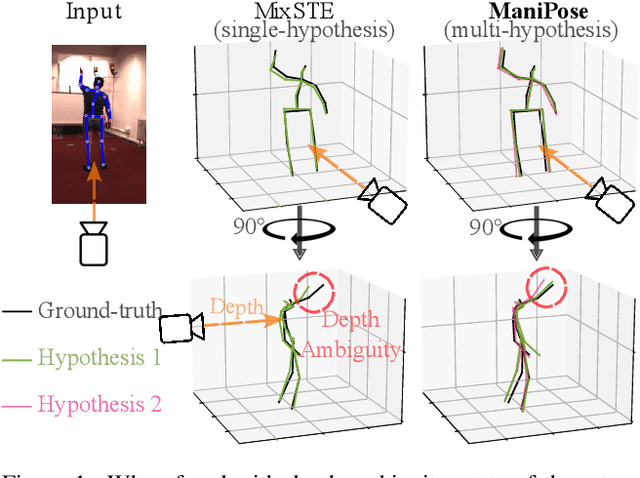
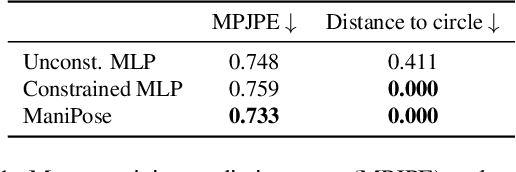
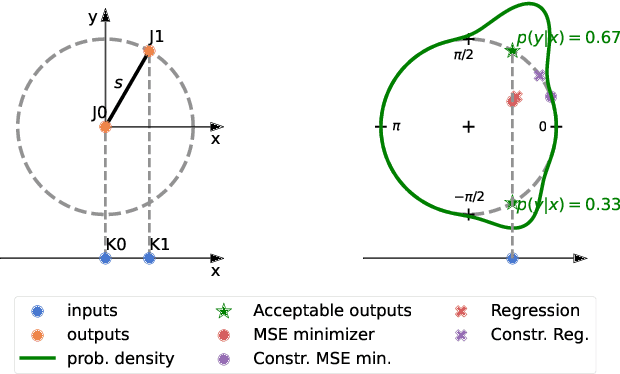
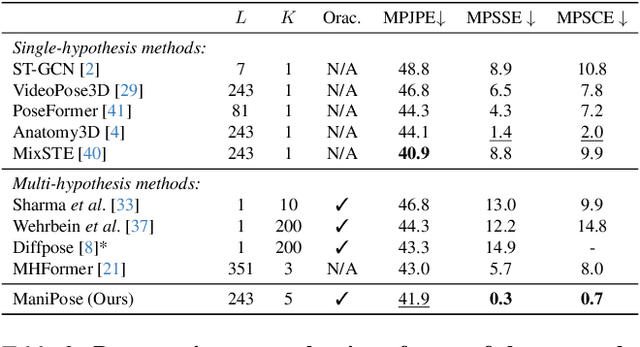
Monocular 3D human pose estimation (3D-HPE) is an inherently ambiguous task, as a 2D pose in an image might originate from different possible 3D poses. Yet, most 3D-HPE methods rely on regression models, which assume a one-to-one mapping between inputs and outputs. In this work, we provide theoretical and empirical evidence that, because of this ambiguity, common regression models are bound to predict topologically inconsistent poses, and that traditional evaluation metrics, such as the MPJPE, P-MPJPE and PCK, are insufficient to assess this aspect. As a solution, we propose ManiPose, a novel manifold-constrained multi-hypothesis model capable of proposing multiple candidate 3D poses for each 2D input, together with their corresponding plausibility. Unlike previous multi-hypothesis approaches, our solution is completely supervised and does not rely on complex generative models, thus greatly facilitating its training and usage. Furthermore, by constraining our model to lie within the human pose manifold, we can guarantee the consistency of all hypothetical poses predicted with our approach, which was not possible in previous works. We illustrate the usefulness of ManiPose in a synthetic 1D-to-2D lifting setting and demonstrate on real-world datasets that it outperforms state-of-the-art models in pose consistency by a large margin, while still reaching competitive MPJPE performance.

DiffHPE: Robust, Coherent 3D Human Pose Lifting with Diffusion

We present an innovative approach to 3D Human Pose Estimation (3D-HPE) by integrating cutting-edge diffusion models, which have revolutionized diverse fields, but are relatively unexplored in 3D-HPE. We show that diffusion models enhance the accuracy, robustness, and coherence of human pose estimations. We introduce DiffHPE, a novel strategy for harnessing diffusion models in 3D-HPE, and demonstrate its ability to refine standard supervised 3D-HPE. We also show how diffusion models lead to more robust estimations in the face of occlusions, and improve the time-coherence and the sagittal symmetry of predictions. Using the Human\,3.6M dataset, we illustrate the effectiveness of our approach and its superiority over existing models, even under adverse situations where the occlusion patterns in training do not match those in inference. Our findings indicate that while standalone diffusion models provide commendable performance, their accuracy is even better in combination with supervised models, opening exciting new avenues for 3D-HPE research.

Data augmentation for learning predictive models on EEG: a systematic comparison

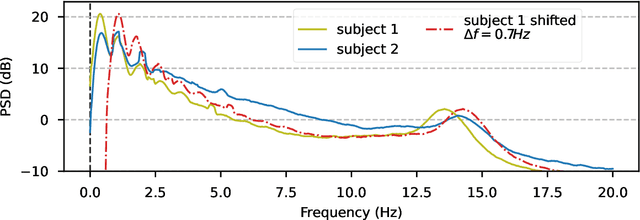
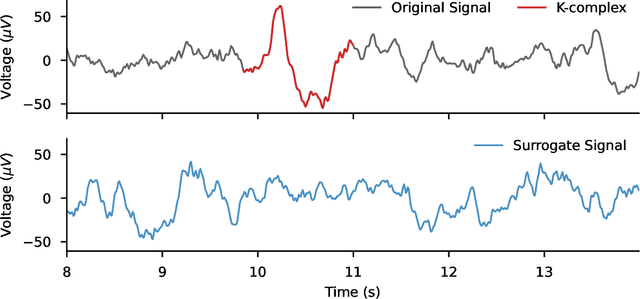
The use of deep learning for electroencephalography (EEG) classification tasks has been rapidly growing in the last years, yet its application has been limited by the relatively small size of EEG datasets. Data augmentation, which consists in artificially increasing the size of the dataset during training, has been a key ingredient to obtain state-of-the-art performances across applications such as computer vision or speech. While a few augmentation transformations for EEG data have been proposed in the literature, their positive impact on performance across tasks remains elusive. In this work, we propose a unified and exhaustive analysis of the main existing EEG augmentations, which are compared in a common experimental setting. Our results highlight the best data augmentations to consider for sleep stage classification and motor imagery brain computer interfaces, showing predictive power improvements greater than 10% in some cases.

Deep invariant networks with differentiable augmentation layers

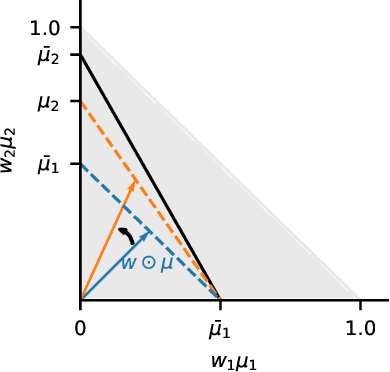
Designing learning systems which are invariant to certain data transformations is critical in machine learning. Practitioners can typically enforce a desired invariance on the trained model through the choice of a network architecture, e.g. using convolutions for translations, or using data augmentation. Yet, enforcing true invariance in the network can be difficult, and data invariances are not always known a piori. State-of-the-art methods for learning data augmentation policies require held-out data and are based on bilevel optimization problems, which are complex to solve and often computationally demanding. In this work we investigate new ways of learning invariances only from the training data. Using learnable augmentation layers built directly in the network, we demonstrate that our method is very versatile. It can incorporate any type of differentiable augmentation and be applied to a broad class of learning problems beyond computer vision. We provide empirical evidence showing that our approach is easier and faster to train than modern automatic data augmentation techniques based on bilevel optimization, while achieving comparable results. Experiments show that while the invariances transferred to a model through automatic data augmentation are limited by the model expressivity, the invariance yielded by our approach is insensitive to it by design.

CADDA: Class-wise Automatic Differentiable Data Augmentation for EEG Signals

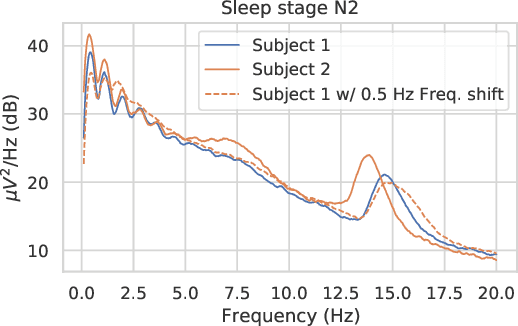
Data augmentation is a key element of deep learning pipelines, as it informs the network during training about transformations of the input data that keep the label unchanged. Manually finding adequate augmentation methods and parameters for a given pipeline is however rapidly cumbersome. In particular, while intuition can guide this decision for images, the design and choice of augmentation policies remains unclear for more complex types of data, such as neuroscience signals. Moreover, label independent strategies might not be suitable for such structured data and class-dependent augmentations might be necessary. This idea has been surprisingly unexplored in the literature, while it is quite intuitive: changing the color of a car image does not change the object class to be predicted, but doing the same to the picture of an orange does. This paper aims to increase the generalization power added through class-wise data augmentation. Yet, as seeking transformations depending on the class largely increases the complexity of the task, using gradient-free optimization techniques as done by most existing automatic approaches becomes intractable for real-world datasets. For this reason we propose to use differentiable data augmentation amenable to gradient-based learning. EEG signals are a perfect example of data for which good augmentation policies are mostly unknown. In this work, we demonstrate the relevance of our approach on the clinically relevant sleep staging classification task, for which we also propose differentiable transformations.