Multiple Choice Learning for Efficient Speech Separation with Many Speakers

Training speech separation models in the supervised setting raises a permutation problem: finding the best assignation between the model predictions and the ground truth separated signals. This inherently ambiguous task is customarily solved using Permutation Invariant Training (PIT). In this article, we instead consider using the Multiple Choice Learning (MCL) framework, which was originally introduced to tackle ambiguous tasks. We demonstrate experimentally on the popular WSJ0-mix and LibriMix benchmarks that MCL matches the performances of PIT, while being computationally advantageous. This opens the door to a promising research direction, as MCL can be naturally extended to handle a variable number of speakers, or to tackle speech separation in the unsupervised setting.

Annealed Multiple Choice Learning: Overcoming limitations of Winner-takes-all with annealing

We introduce Annealed Multiple Choice Learning (aMCL) which combines simulated annealing with MCL. MCL is a learning framework handling ambiguous tasks by predicting a small set of plausible hypotheses. These hypotheses are trained using the Winner-takes-all (WTA) scheme, which promotes the diversity of the predictions. However, this scheme may converge toward an arbitrarily suboptimal local minimum, due to the greedy nature of WTA. We overcome this limitation using annealing, which enhances the exploration of the hypothesis space during training. We leverage insights from statistical physics and information theory to provide a detailed description of the model training trajectory. Additionally, we validate our algorithm by extensive experiments on synthetic datasets, on the standard UCI benchmark, and on speech separation.

Winner-takes-all learners are geometry-aware conditional density estimators

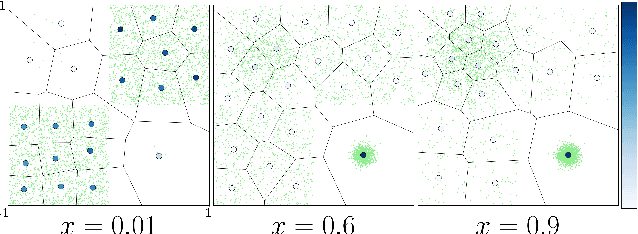
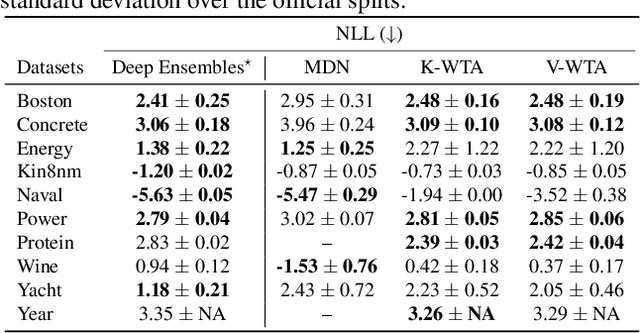
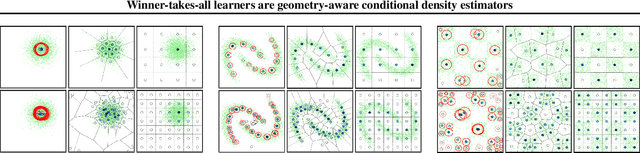
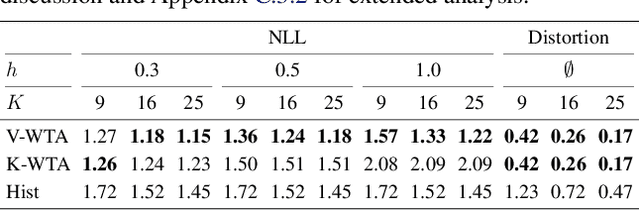
Winner-takes-all training is a simple learning paradigm, which handles ambiguous tasks by predicting a set of plausible hypotheses. Recently, a connection was established between Winner-takes-all training and centroidal Voronoi tessellations, showing that, once trained, hypotheses should quantize optimally the shape of the conditional distribution to predict. However, the best use of these hypotheses for uncertainty quantification is still an open question.In this work, we show how to leverage the appealing geometric properties of the Winner-takes-all learners for conditional density estimation, without modifying its original training scheme. We theoretically establish the advantages of our novel estimator both in terms of quantization and density estimation, and we demonstrate its competitiveness on synthetic and real-world datasets, including audio data.