Byeongsu Sim
PLADIS: Pushing the Limits of Attention in Diffusion Models at Inference Time by Leveraging Sparsity
Mar 10, 2025
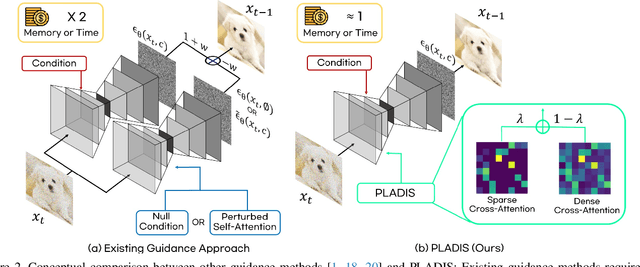
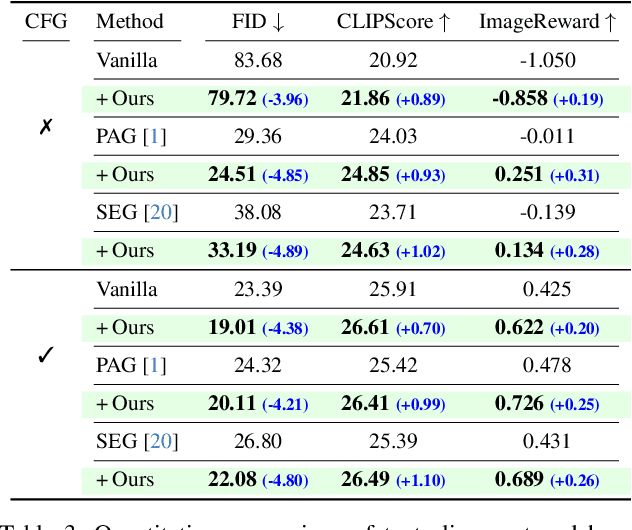

Abstract:Diffusion models have shown impressive results in generating high-quality conditional samples using guidance techniques such as Classifier-Free Guidance (CFG). However, existing methods often require additional training or neural function evaluations (NFEs), making them incompatible with guidance-distilled models. Also, they rely on heuristic approaches that need identifying target layers. In this work, we propose a novel and efficient method, termed PLADIS, which boosts pre-trained models (U-Net/Transformer) by leveraging sparse attention. Specifically, we extrapolate query-key correlations using softmax and its sparse counterpart in the cross-attention layer during inference, without requiring extra training or NFEs. By leveraging the noise robustness of sparse attention, our PLADIS unleashes the latent potential of text-to-image diffusion models, enabling them to excel in areas where they once struggled with newfound effectiveness. It integrates seamlessly with guidance techniques, including guidance-distilled models. Extensive experiments show notable improvements in text alignment and human preference, offering a highly efficient and universally applicable solution.
Derivative-Free Diffusion Manifold-Constrained Gradient for Unified XAI
Nov 22, 2024

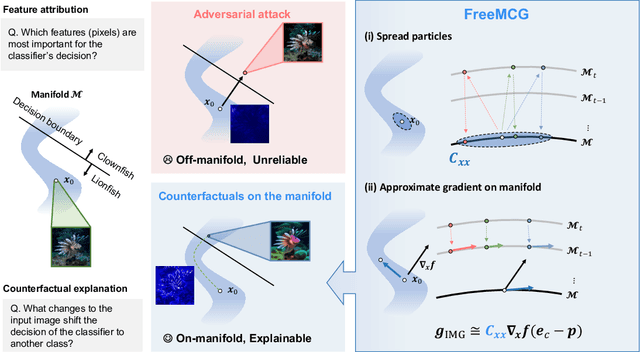
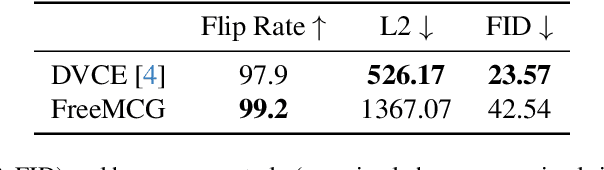
Abstract:Gradient-based methods are a prototypical family of explainability techniques, especially for image-based models. Nonetheless, they have several shortcomings in that they (1) require white-box access to models, (2) are vulnerable to adversarial attacks, and (3) produce attributions that lie off the image manifold, leading to explanations that are not actually faithful to the model and do not align well with human perception. To overcome these challenges, we introduce Derivative-Free Diffusion Manifold-Constrainted Gradients (FreeMCG), a novel method that serves as an improved basis for explainability of a given neural network than the traditional gradient. Specifically, by leveraging ensemble Kalman filters and diffusion models, we derive a derivative-free approximation of the model's gradient projected onto the data manifold, requiring access only to the model's outputs. We demonstrate the effectiveness of FreeMCG by applying it to both counterfactual generation and feature attribution, which have traditionally been treated as distinct tasks. Through comprehensive evaluation on both tasks, counterfactual explanation and feature attribution, we show that our method yields state-of-the-art results while preserving the essential properties expected of XAI tools.
Magnitude and Angle Dynamics in Training Single ReLU Neurons
Oct 12, 2022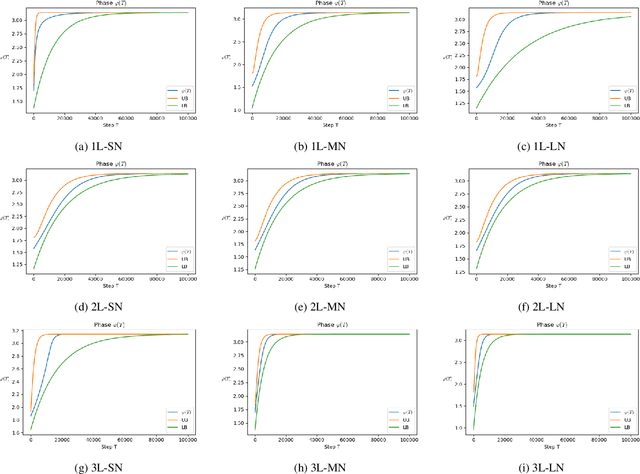
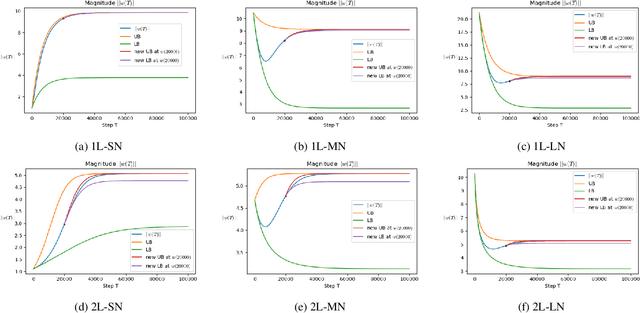
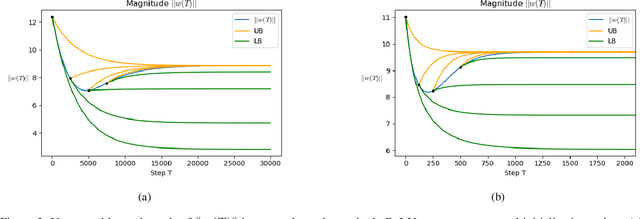
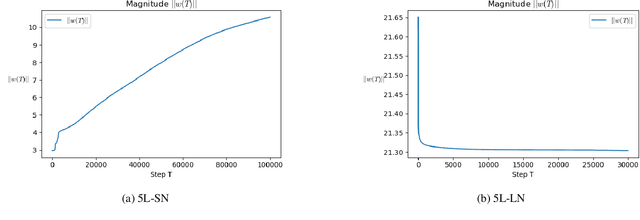
Abstract:To understand learning the dynamics of deep ReLU networks, we investigate the dynamic system of gradient flow $w(t)$ by decomposing it to magnitude $w(t)$ and angle $\phi(t):= \pi - \theta(t) $ components. In particular, for multi-layer single ReLU neurons with spherically symmetric data distribution and the square loss function, we provide upper and lower bounds for magnitude and angle components to describe the dynamics of gradient flow. Using the obtained bounds, we conclude that small scale initialization induces slow convergence speed for deep single ReLU neurons. Finally, by exploiting the relation of gradient flow and gradient descent, we extend our results to the gradient descent approach. All theoretical results are verified by experiments.
Improving Diffusion Models for Inverse Problems using Manifold Constraints
Jun 02, 2022
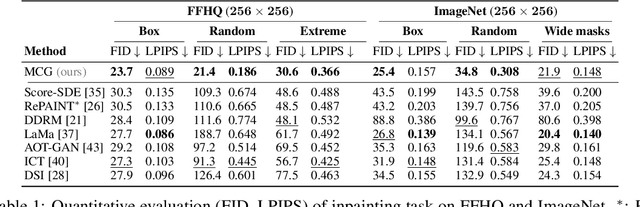
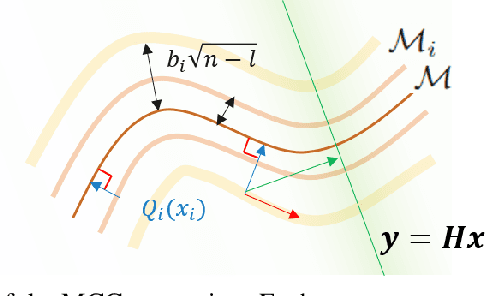

Abstract:Recently, diffusion models have been used to solve various inverse problems in an unsupervised manner with appropriate modifications to the sampling process. However, the current solvers, which recursively apply a reverse diffusion step followed by a measurement consistency step, often produce sub-optimal results. By studying the generative sampling path, here we show that current solvers throw the sample path off the data manifold, and hence the error accumulates. To address this, we propose an additional correction term inspired by the manifold constraint, which can be used synergistically with the previous solvers to make the iterations close to the manifold. The proposed manifold constraint is straightforward to implement within a few lines of code, yet boosts the performance by a surprisingly large margin. With extensive experiments, we show that our method is superior to the previous methods both theoretically and empirically, producing promising results in many applications such as image inpainting, colorization, and sparse-view computed tomography.
Support Vectors and Gradient Dynamics for Implicit Bias in ReLU Networks
Feb 11, 2022

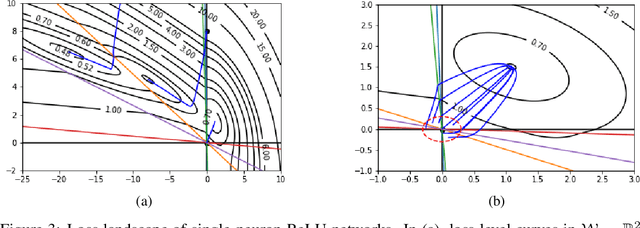
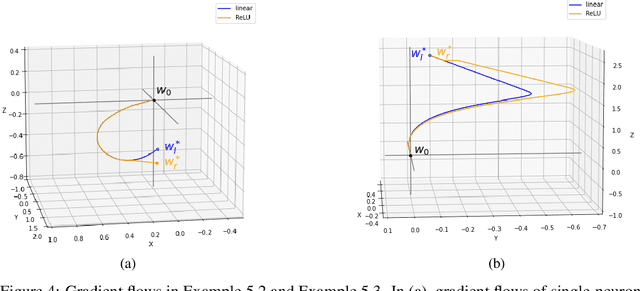
Abstract:Understanding implicit bias of gradient descent has been an important goal in machine learning research. Unfortunately, even for a single-neuron ReLU network, it recently proved impossible to characterize the implicit regularization with the square loss by an explicit function of the norm of model parameters. In order to close the gap between the existing theory and the intriguing empirical behavior of ReLU networks, here we examine the gradient flow dynamics in the parameter space when training single-neuron ReLU networks. Specifically, we discover implicit bias in terms of support vectors in ReLU networks, which play a key role in why and how ReLU networks generalize well. Moreover, we analyze gradient flows with respect to the magnitude of the norm of initialization, and show the impact of the norm in gradient dynamics. Lastly, under some conditions, we prove that the norm of the learned weight strictly increases on the gradient flow.
Come-Closer-Diffuse-Faster: Accelerating Conditional Diffusion Models for Inverse Problems through Stochastic Contraction
Dec 09, 2021



Abstract:Diffusion models have recently attained significant interest within the community owing to their strong performance as generative models. Furthermore, its application to inverse problems have demonstrated state-of-the-art performance. Unfortunately, diffusion models have a critical downside - they are inherently slow to sample from, needing few thousand steps of iteration to generate images from pure Gaussian noise. In this work, we show that starting from Gaussian noise is unnecessary. Instead, starting from a single forward diffusion with better initialization significantly reduces the number of sampling steps in the reverse conditional diffusion. This phenomenon is formally explained by the contraction theory of the stochastic difference equations like our conditional diffusion strategy - the alternating applications of reverse diffusion followed by a non-expansive data consistency step. The new sampling strategy, dubbed Come-Closer-Diffuse-Faster (CCDF), also reveals a new insight on how the existing feed-forward neural network approaches for inverse problems can be synergistically combined with the diffusion models. Experimental results with super-resolution, image inpainting, and compressed sensing MRI demonstrate that our method can achieve state-of-the-art reconstruction performance at significantly reduced sampling steps.
Unpaired Deep Learning for Accelerated MRI using Optimal Transport Driven CycleGAN
Aug 29, 2020

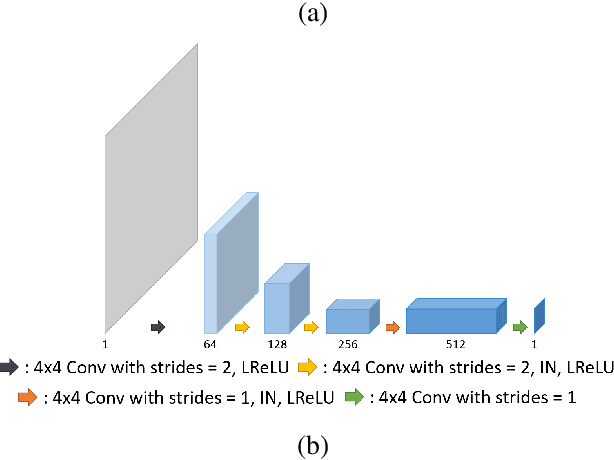

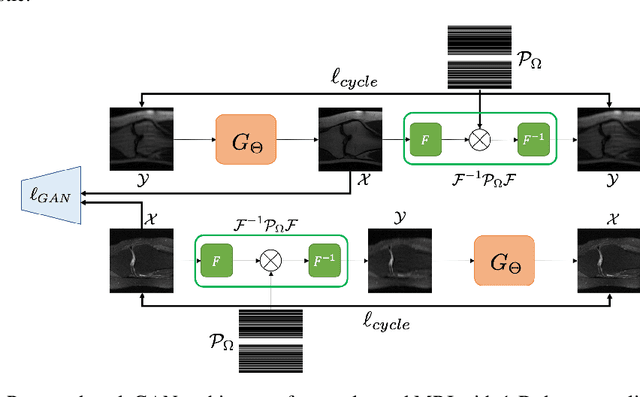
Abstract:Recently, deep learning approaches for accelerated MRI have been extensively studied thanks to their high performance reconstruction in spite of significantly reduced runtime complexity. These neural networks are usually trained in a supervised manner, so matched pairs of subsampled and fully sampled k-space data are required. Unfortunately, it is often difficult to acquire matched fully sampled k-space data, since the acquisition of fully sampled k-space data requires long scan time and often leads to the change of the acquisition protocol. Therefore, unpaired deep learning without matched label data has become a very important research topic. In this paper, we propose an unpaired deep learning approach using a optimal transport driven cycle-consistent generative adversarial network (OT-cycleGAN) that employs a single pair of generator and discriminator. The proposed OT-cycleGAN architecture is rigorously derived from a dual formulation of the optimal transport formulation using a specially designed penalized least squares cost. The experimental results show that our method can reconstruct high resolution MR images from accelerated k- space data from both single and multiple coil acquisition, without requiring matched reference data.
Optimal Transport, CycleGAN, and Penalized LS for Unsupervised Learning in Inverse Problems
Sep 25, 2019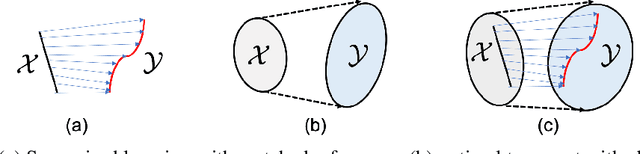

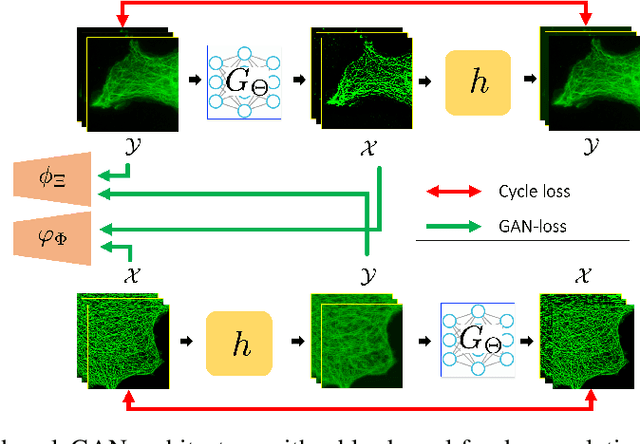
Abstract:The penalized least squares (PLS) is a classic approach to inverse problems, where a regularization term is added to stabilize the solution. Optimal transport (OT) is another mathematical framework for computer vision tasks by providing means to transport one measure to another at a minimal cost. Cycle-consistent generative adversarial network (cycleGAN) is a recent extension of GAN to learn target distributions with less mode collapsing behaviour. Although similar in that no supervised training is required, the algorithms look different, so the mathematical relationship between these approaches is not clear. In this article, we provide an important advance to unveil the missing link. Specifically, we reveal that a cycleGAN architecture can be derived as a dual formulation of the optimal transport problem, if the PLS with a deep learning penalty is used as a transport cost between the two probability measures from measurements and unknown images. This suggests that cycleGAN can be considered as a stochastic generalization of classical PLS approaches. Our derivation is so general that various types of cycleGAN architecture can be easily derived by merely changing the transport cost. As proofs of concept, this paper provides novel cycleGAN architecture for unsupervised learning in accelerated MRI and deconvolution microscopy problems, which confirm the efficacy and the flexibility of the theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge