Optimal Transport, CycleGAN, and Penalized LS for Unsupervised Learning in Inverse Problems

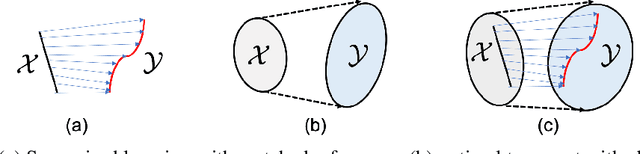
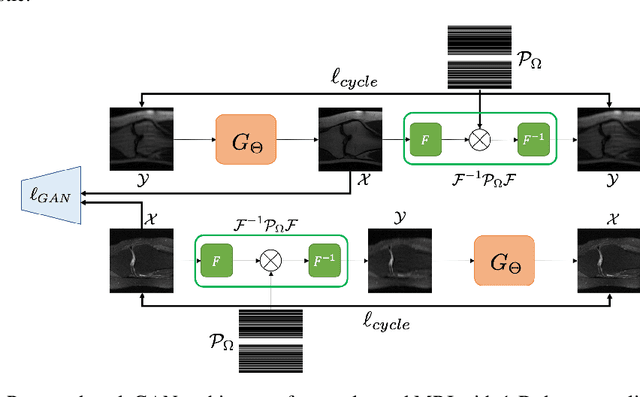
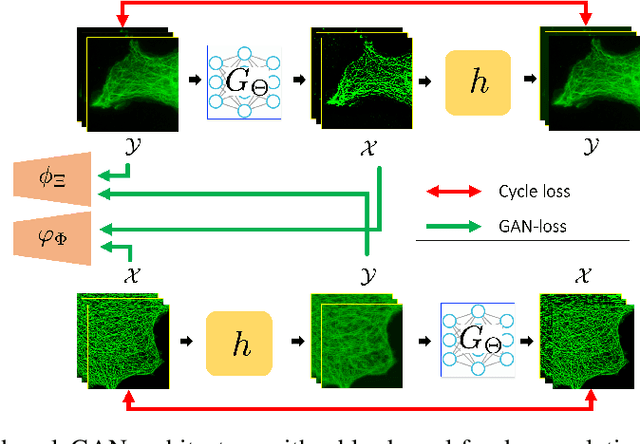
The penalized least squares (PLS) is a classic approach to inverse problems, where a regularization term is added to stabilize the solution. Optimal transport (OT) is another mathematical framework for computer vision tasks by providing means to transport one measure to another at a minimal cost. Cycle-consistent generative adversarial network (cycleGAN) is a recent extension of GAN to learn target distributions with less mode collapsing behaviour. Although similar in that no supervised training is required, the algorithms look different, so the mathematical relationship between these approaches is not clear. In this article, we provide an important advance to unveil the missing link. Specifically, we reveal that a cycleGAN architecture can be derived as a dual formulation of the optimal transport problem, if the PLS with a deep learning penalty is used as a transport cost between the two probability measures from measurements and unknown images. This suggests that cycleGAN can be considered as a stochastic generalization of classical PLS approaches. Our derivation is so general that various types of cycleGAN architecture can be easily derived by merely changing the transport cost. As proofs of concept, this paper provides novel cycleGAN architecture for unsupervised learning in accelerated MRI and deconvolution microscopy problems, which confirm the efficacy and the flexibility of the theory.