Support Vectors and Gradient Dynamics for Implicit Bias in ReLU Networks
Paper and Code
Feb 11, 2022

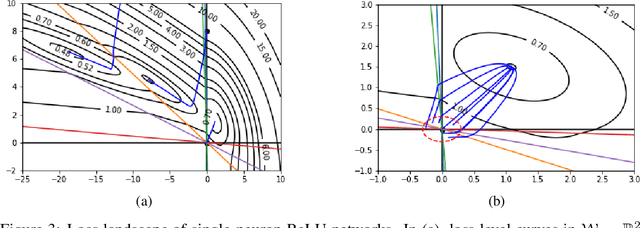
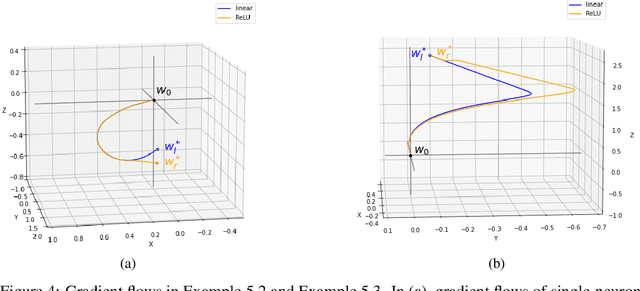
Understanding implicit bias of gradient descent has been an important goal in machine learning research. Unfortunately, even for a single-neuron ReLU network, it recently proved impossible to characterize the implicit regularization with the square loss by an explicit function of the norm of model parameters. In order to close the gap between the existing theory and the intriguing empirical behavior of ReLU networks, here we examine the gradient flow dynamics in the parameter space when training single-neuron ReLU networks. Specifically, we discover implicit bias in terms of support vectors in ReLU networks, which play a key role in why and how ReLU networks generalize well. Moreover, we analyze gradient flows with respect to the magnitude of the norm of initialization, and show the impact of the norm in gradient dynamics. Lastly, under some conditions, we prove that the norm of the learned weight strictly increases on the gradient flow.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge