Magnitude and Angle Dynamics in Training Single ReLU Neurons
Paper and Code
Oct 12, 2022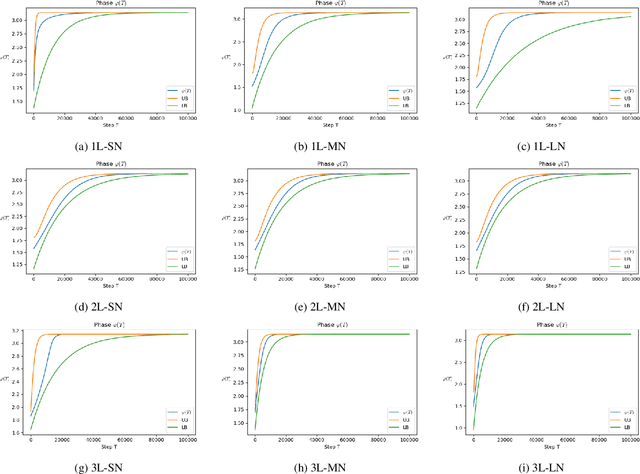
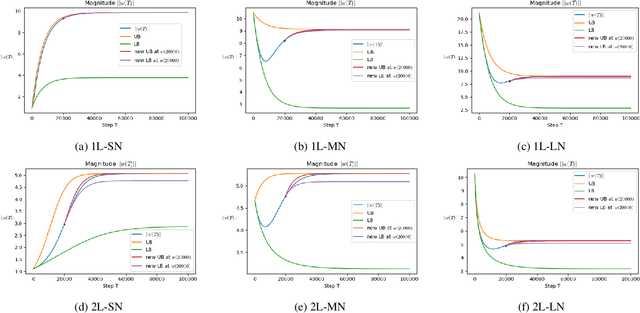
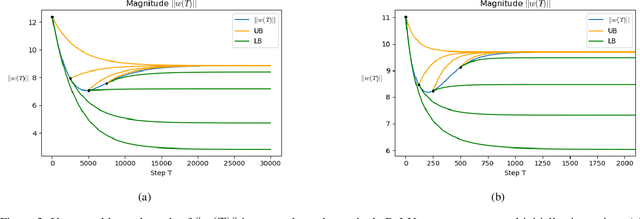
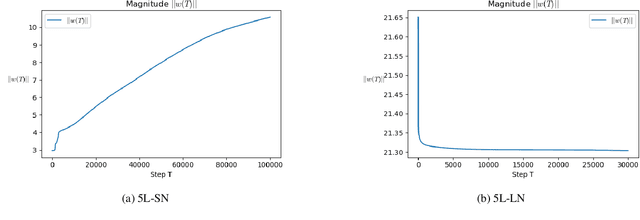
To understand learning the dynamics of deep ReLU networks, we investigate the dynamic system of gradient flow $w(t)$ by decomposing it to magnitude $w(t)$ and angle $\phi(t):= \pi - \theta(t) $ components. In particular, for multi-layer single ReLU neurons with spherically symmetric data distribution and the square loss function, we provide upper and lower bounds for magnitude and angle components to describe the dynamics of gradient flow. Using the obtained bounds, we conclude that small scale initialization induces slow convergence speed for deep single ReLU neurons. Finally, by exploiting the relation of gradient flow and gradient descent, we extend our results to the gradient descent approach. All theoretical results are verified by experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge