Image Registration and Predictive Modeling: Learning the Metric on the Space of Diffeomorphisms

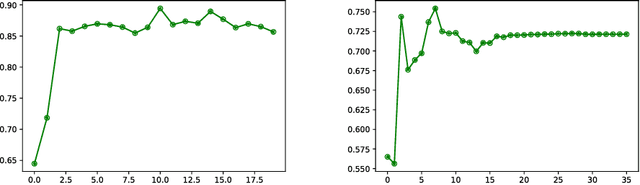
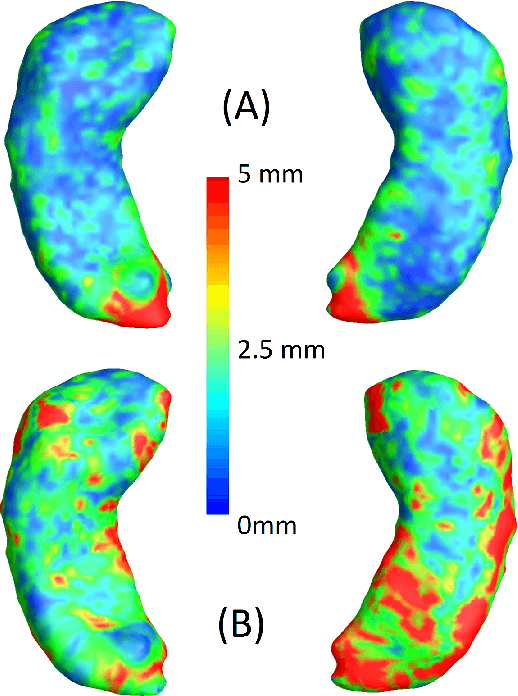
We present a method for metric optimization in the Large Deformation Diffeomorphic Metric Mapping (LDDMM) framework, by treating the induced Riemannian metric on the space of diffeomorphisms as a kernel in a machine learning context. For simplicity, we choose the kernel Fischer Linear Discriminant Analysis (KLDA) as the framework. Optimizing the kernel parameters in an Expectation-Maximization framework, we define model fidelity via the hinge loss of the decision function. The resulting algorithm optimizes the parameters of the LDDMM norm-inducing differential operator as a solution to a group-wise registration and classification problem. In practice, this may lead to a biology-aware registration, focusing its attention on the predictive task at hand such as identifying the effects of disease. We first tested our algorithm on a synthetic dataset, showing that our parameter selection improves registration quality and classification accuracy. We then tested the algorithm on 3D subcortical shapes from the Schizophrenia cohort Schizconnect. Our Schizpohrenia-Control predictive model showed significant improvement in ROC AUC compared to baseline parameters.

Simultaneous Matrix Diagonalization for Structural Brain Networks Classification

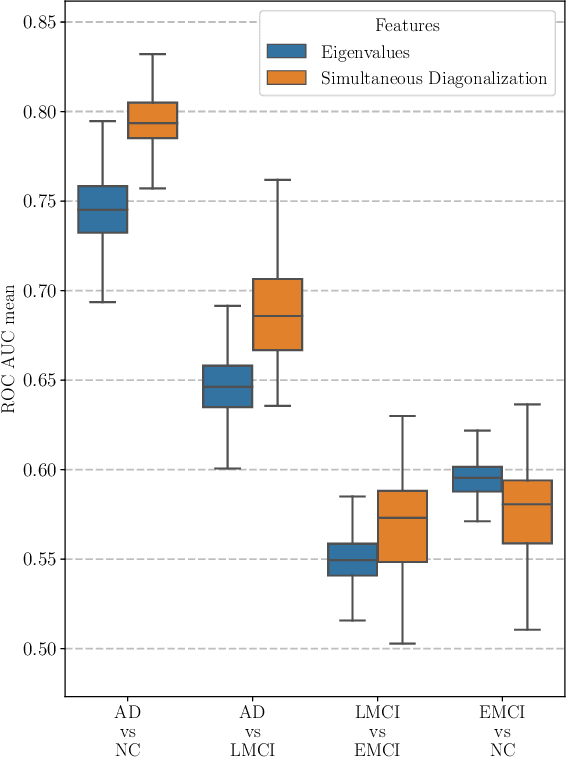
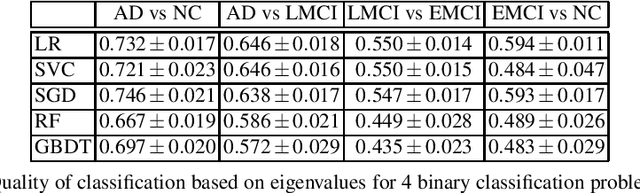
This paper considers the problem of brain disease classification based on connectome data. A connectome is a network representation of a human brain. The typical connectome classification problem is very challenging because of the small sample size and high dimensionality of the data. We propose to use simultaneous approximate diagonalization of adjacency matrices in order to compute their eigenstructures in more stable way. The obtained approximate eigenvalues are further used as features for classification. The proposed approach is demonstrated to be efficient for detection of Alzheimer's disease, outperforming simple baselines and competing with state-of-the-art approaches to brain disease classification.

An Empirical Study of Continuous Connectivity Degree Sequence Equivalents

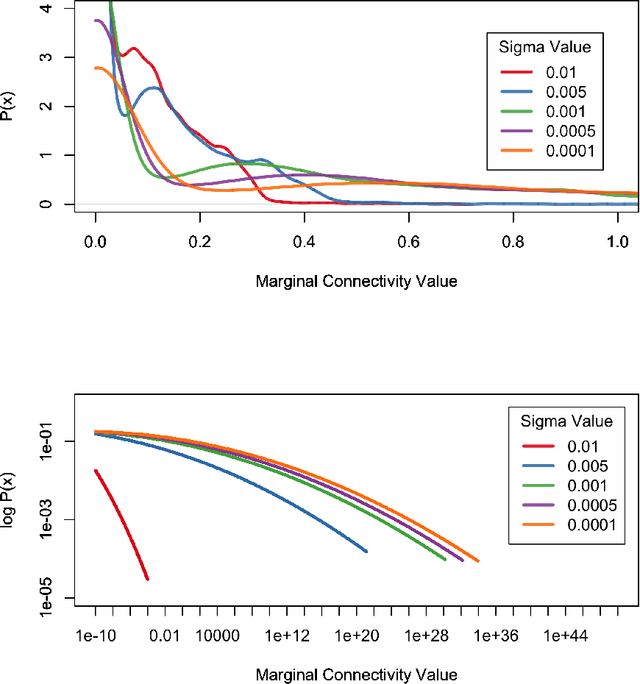
In the present work we demonstrate the use of a parcellation free connectivity model based on Poisson point processes. This model produces for each subject a continuous bivariate intensity function that represents for every possible pair of points the relative rate at which we observe tracts terminating at those points. We fit this model to explore degree sequence equivalents for spatial continuum graphs, and to investigate the local differences between estimated intensity functions for two different tractography methods. This is a companion paper to Moyer et al. (2016), where the model was originally defined.