On the properties of some low-parameter models for color reproduction in terms of spectrum transformations and coverage of a color triangle

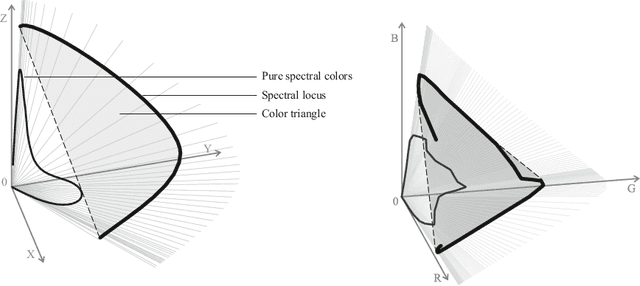
One of the classical approaches to solving color reproduction problems, such as color adaptation or color space transform, is the use of low-parameter spectral models. The strength of this approach is the ability to choose a set of properties that the model should have, be it a large coverage area of a color triangle, an accurate description of the addition or multiplication of spectra, knowing only the tristimulus corresponding to them. The disadvantage is that some of the properties of the mentioned spectral models are confirmed only experimentally. This work is devoted to the theoretical substantiation of various properties of spectral models. In particular, we prove that the banded model is the only model that simultaneously possesses the properties of closure under addition and multiplication. We also show that the Gaussian model is the limiting case of the von Mises model and prove that the set of protomers of the von Mises model unambiguously covers the color triangle in both the case of convex and non-convex spectral locus.

Robust $k$-means Clustering for Distributions with Two Moments

We consider the robust algorithms for the $k$-means clustering problem where a quantizer is constructed based on $N$ independent observations. Our main results are median of means based non-asymptotic excess distortion bounds that hold under the two bounded moments assumption in a general separable Hilbert space. In particular, our results extend the renowned asymptotic result of Pollard, 1981 who showed that the existence of two moments is sufficient for strong consistency of an empirically optimal quantizer in $\mathbb{R}^d$. In a special case of clustering in $\mathbb{R}^d$, under two bounded moments, we prove matching (up to constant factors) non-asymptotic upper and lower bounds on the excess distortion, which depend on the probability mass of the lightest cluster of an optimal quantizer. Our bounds have the sub-Gaussian form, and the proofs are based on the versions of uniform bounds for robust mean estimators.

Image Registration and Predictive Modeling: Learning the Metric on the Space of Diffeomorphisms

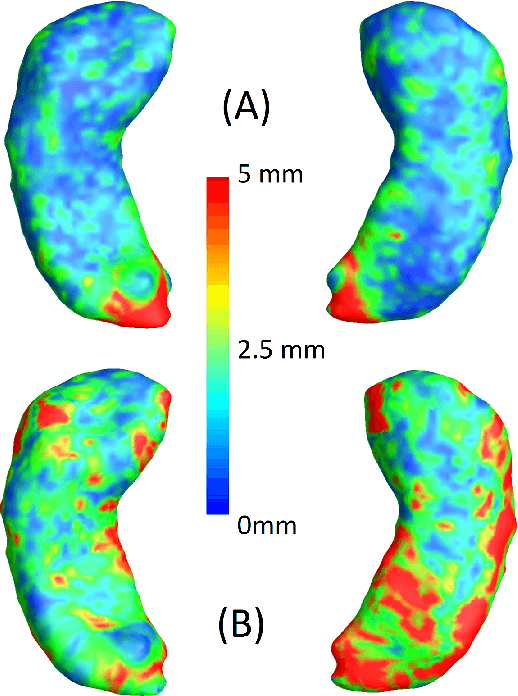
We present a method for metric optimization in the Large Deformation Diffeomorphic Metric Mapping (LDDMM) framework, by treating the induced Riemannian metric on the space of diffeomorphisms as a kernel in a machine learning context. For simplicity, we choose the kernel Fischer Linear Discriminant Analysis (KLDA) as the framework. Optimizing the kernel parameters in an Expectation-Maximization framework, we define model fidelity via the hinge loss of the decision function. The resulting algorithm optimizes the parameters of the LDDMM norm-inducing differential operator as a solution to a group-wise registration and classification problem. In practice, this may lead to a biology-aware registration, focusing its attention on the predictive task at hand such as identifying the effects of disease. We first tested our algorithm on a synthetic dataset, showing that our parameter selection improves registration quality and classification accuracy. We then tested the algorithm on 3D subcortical shapes from the Schizophrenia cohort Schizconnect. Our Schizpohrenia-Control predictive model showed significant improvement in ROC AUC compared to baseline parameters.