RClicks: Realistic Click Simulation for Benchmarking Interactive Segmentation

The emergence of Segment Anything (SAM) sparked research interest in the field of interactive segmentation, especially in the context of image editing tasks and speeding up data annotation. Unlike common semantic segmentation, interactive segmentation methods allow users to directly influence their output through prompts (e.g. clicks). However, click patterns in real-world interactive segmentation scenarios remain largely unexplored. Most methods rely on the assumption that users would click in the center of the largest erroneous area. Nevertheless, recent studies show that this is not always the case. Thus, methods may have poor performance in real-world deployment despite high metrics in a baseline benchmark. To accurately simulate real-user clicks, we conducted a large crowdsourcing study of click patterns in an interactive segmentation scenario and collected 475K real-user clicks. Drawing on ideas from saliency tasks, we develop a clickability model that enables sampling clicks, which closely resemble actual user inputs. Using our model and dataset, we propose RClicks benchmark for a comprehensive comparison of existing interactive segmentation methods on realistic clicks. Specifically, we evaluate not only the average quality of methods, but also the robustness w.r.t. click patterns. According to our benchmark, in real-world usage interactive segmentation models may perform worse than it has been reported in the baseline benchmark, and most of the methods are not robust. We believe that RClicks is a significant step towards creating interactive segmentation methods that provide the best user experience in real-world cases.

TETRIS: Towards Exploring the Robustness of Interactive Segmentation

Interactive segmentation methods rely on user inputs to iteratively update the selection mask. A click specifying the object of interest is arguably the most simple and intuitive interaction type, and thereby the most common choice for interactive segmentation. However, user clicking patterns in the interactive segmentation context remain unexplored. Accordingly, interactive segmentation evaluation strategies rely more on intuition and common sense rather than empirical studies (e.g., assuming that users tend to click in the center of the area with the largest error). In this work, we conduct a real user study to investigate real user clicking patterns. This study reveals that the intuitive assumption made in the common evaluation strategy may not hold. As a result, interactive segmentation models may show high scores in the standard benchmarks, but it does not imply that they would perform well in a real world scenario. To assess the applicability of interactive segmentation methods, we propose a novel evaluation strategy providing a more comprehensive analysis of a model's performance. To this end, we propose a methodology for finding extreme user inputs by a direct optimization in a white-box adversarial attack on the interactive segmentation model. Based on the performance with such adversarial user inputs, we assess the robustness of interactive segmentation models w.r.t click positions. Besides, we introduce a novel benchmark for measuring the robustness of interactive segmentation, and report the results of an extensive evaluation of dozens of models.

On the properties of some low-parameter models for color reproduction in terms of spectrum transformations and coverage of a color triangle

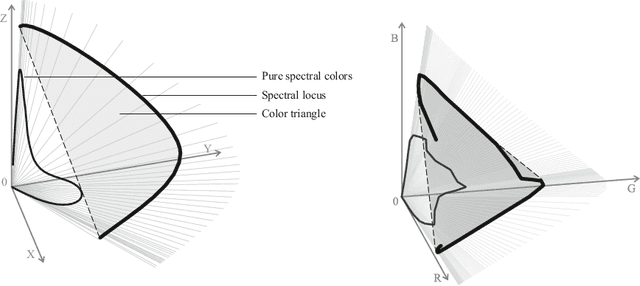
One of the classical approaches to solving color reproduction problems, such as color adaptation or color space transform, is the use of low-parameter spectral models. The strength of this approach is the ability to choose a set of properties that the model should have, be it a large coverage area of a color triangle, an accurate description of the addition or multiplication of spectra, knowing only the tristimulus corresponding to them. The disadvantage is that some of the properties of the mentioned spectral models are confirmed only experimentally. This work is devoted to the theoretical substantiation of various properties of spectral models. In particular, we prove that the banded model is the only model that simultaneously possesses the properties of closure under addition and multiplication. We also show that the Gaussian model is the limiting case of the von Mises model and prove that the set of protomers of the von Mises model unambiguously covers the color triangle in both the case of convex and non-convex spectral locus.