Image Registration and Predictive Modeling: Learning the Metric on the Space of Diffeomorphisms

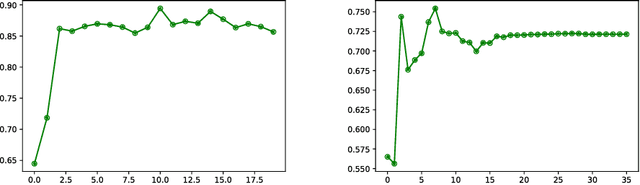
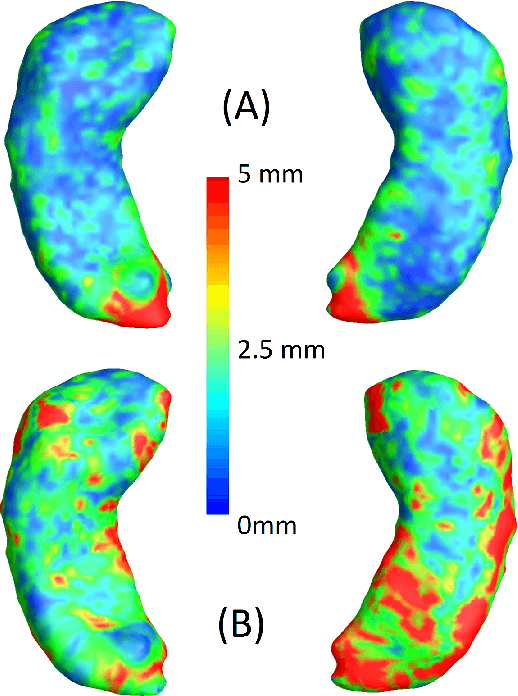
We present a method for metric optimization in the Large Deformation Diffeomorphic Metric Mapping (LDDMM) framework, by treating the induced Riemannian metric on the space of diffeomorphisms as a kernel in a machine learning context. For simplicity, we choose the kernel Fischer Linear Discriminant Analysis (KLDA) as the framework. Optimizing the kernel parameters in an Expectation-Maximization framework, we define model fidelity via the hinge loss of the decision function. The resulting algorithm optimizes the parameters of the LDDMM norm-inducing differential operator as a solution to a group-wise registration and classification problem. In practice, this may lead to a biology-aware registration, focusing its attention on the predictive task at hand such as identifying the effects of disease. We first tested our algorithm on a synthetic dataset, showing that our parameter selection improves registration quality and classification accuracy. We then tested the algorithm on 3D subcortical shapes from the Schizophrenia cohort Schizconnect. Our Schizpohrenia-Control predictive model showed significant improvement in ROC AUC compared to baseline parameters.

Residual and Plain Convolutional Neural Networks for 3D Brain MRI Classification

In the recent years there have been a number of studies that applied deep learning algorithms to neuroimaging data. Pipelines used in those studies mostly require multiple processing steps for feature extraction, although modern advancements in deep learning for image classification can provide a powerful framework for automatic feature generation and more straightforward analysis. In this paper, we show how similar performance can be achieved skipping these feature extraction steps with the residual and plain 3D convolutional neural network architectures. We demonstrate the performance of the proposed approach for classification of Alzheimer's disease versus mild cognitive impairment and normal controls on the Alzheimer's Disease National Initiative (ADNI) dataset of 3D structural MRI brain scans.

Kernel classification of connectomes based on earth mover's distance between graph spectra

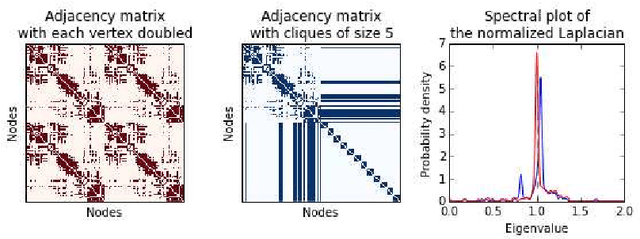
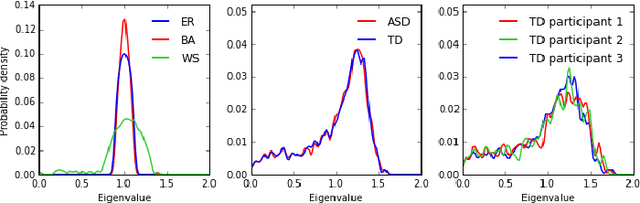
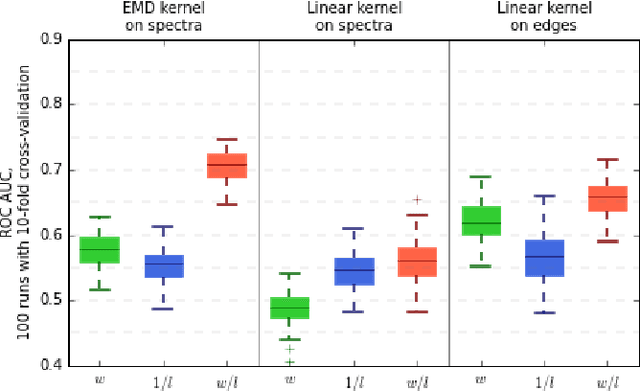
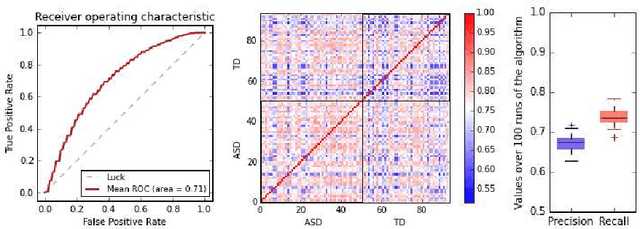
In this paper, we tackle a problem of predicting phenotypes from structural connectomes. We propose that normalized Laplacian spectra can capture structural properties of brain networks, and hence graph spectral distributions are useful for a task of connectome-based classification. We introduce a kernel that is based on earth mover's distance (EMD) between spectral distributions of brain networks. We access performance of an SVM classifier with the proposed kernel for a task of classification of autism spectrum disorder versus typical development based on a publicly available dataset. Classification quality (area under the ROC-curve) obtained with the EMD-based kernel on spectral distributions is 0.71, which is higher than that based on simpler graph embedding methods.