Geometry-Aware Maximum Likelihood Estimation of Intrinsic Dimension

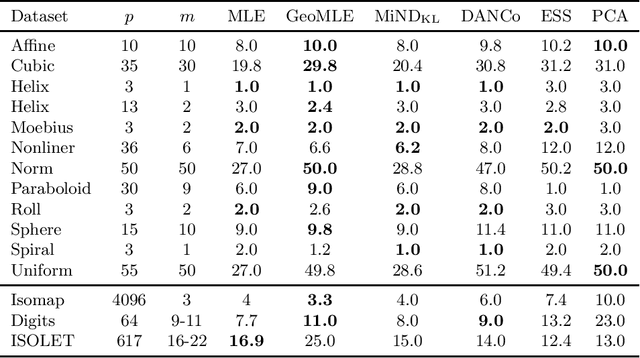
The existing approaches to intrinsic dimension estimation usually are not reliable when the data are nonlinearly embedded in the high dimensional space. In this work, we show that the explicit accounting to geometric properties of unknown support leads to the polynomial correction to the standard maximum likelihood estimate of intrinsic dimension for flat manifolds. The proposed algorithm (GeoMLE) realizes the correction by regression of standard MLEs based on distances to nearest neighbors for different sizes of neighborhoods. Moreover, the proposed approach also efficiently handles the case of nonuniform sampling of the manifold. We perform numerous experiments on different synthetic and real-world datasets. The results show that our algorithm achieves state-of-the-art performance, while also being computationally efficient and robust to noise in the data.

Simultaneous Matrix Diagonalization for Structural Brain Networks Classification

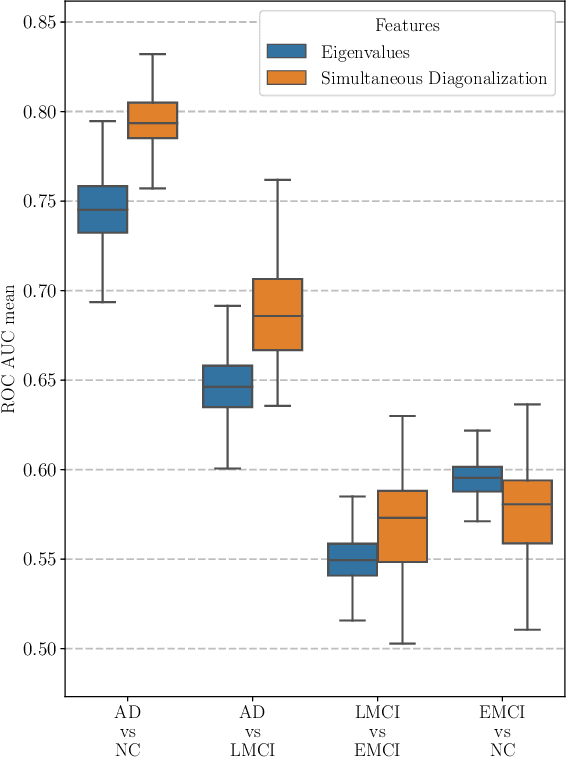
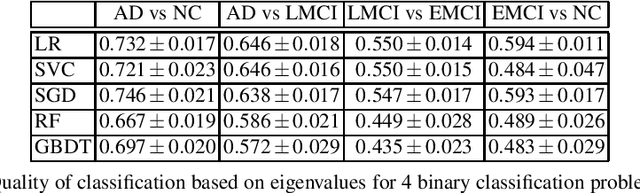
This paper considers the problem of brain disease classification based on connectome data. A connectome is a network representation of a human brain. The typical connectome classification problem is very challenging because of the small sample size and high dimensionality of the data. We propose to use simultaneous approximate diagonalization of adjacency matrices in order to compute their eigenstructures in more stable way. The obtained approximate eigenvalues are further used as features for classification. The proposed approach is demonstrated to be efficient for detection of Alzheimer's disease, outperforming simple baselines and competing with state-of-the-art approaches to brain disease classification.