DIT: Dimension Reduction View on Optimal NFT Rarity Meters

Non-fungible tokens (NFTs) have become a significant digital asset class, each uniquely representing virtual entities such as artworks. These tokens are stored in collections within smart contracts and are actively traded across platforms on Ethereum, Bitcoin, and Solana blockchains. The value of NFTs is closely tied to their distinctive characteristics that define rarity, leading to a growing interest in quantifying rarity within both industry and academia. While there are existing rarity meters for assessing NFT rarity, comparing them can be challenging without direct access to the underlying collection data. The Rating over all Rarities (ROAR) benchmark addresses this challenge by providing a standardized framework for evaluating NFT rarity. This paper explores a dimension reduction approach to rarity design, introducing new performance measures and meters, and evaluates them using the ROAR benchmark. Our contributions to the rarity meter design issue include developing an optimal rarity meter design using non-metric weighted multidimensional scaling, introducing Dissimilarity in Trades (DIT) as a performance measure inspired by dimension reduction techniques, and unveiling the non-interpretable rarity meter DIT, which demonstrates superior performance compared to existing methods.

Geometry-Aware Maximum Likelihood Estimation of Intrinsic Dimension

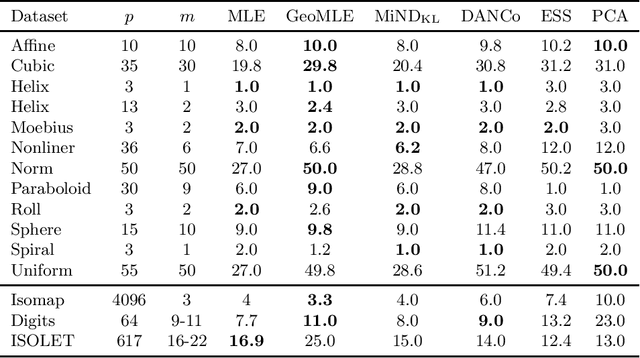
The existing approaches to intrinsic dimension estimation usually are not reliable when the data are nonlinearly embedded in the high dimensional space. In this work, we show that the explicit accounting to geometric properties of unknown support leads to the polynomial correction to the standard maximum likelihood estimate of intrinsic dimension for flat manifolds. The proposed algorithm (GeoMLE) realizes the correction by regression of standard MLEs based on distances to nearest neighbors for different sizes of neighborhoods. Moreover, the proposed approach also efficiently handles the case of nonuniform sampling of the manifold. We perform numerous experiments on different synthetic and real-world datasets. The results show that our algorithm achieves state-of-the-art performance, while also being computationally efficient and robust to noise in the data.

Machine Learning in Appearance-based Robot Self-localization

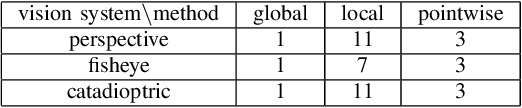
An appearance-based robot self-localization problem is considered in the machine learning framework. The appearance space is composed of all possible images, which can be captured by a robot's visual system under all robot localizations. Using recent manifold learning and deep learning techniques, we propose a new geometrically motivated solution based on training data consisting of a finite set of images captured in known locations of the robot. The solution includes estimation of the robot localization mapping from the appearance space to the robot localization space, as well as estimation of the inverse mapping for modeling visual image features. The latter allows solving the robot localization problem as the Kalman filtering problem.