Distance Based Image Classification: A solution to generative classification's conundrum?

Most classifiers rely on discriminative boundaries that separate instances of each class from everything else. We argue that discriminative boundaries are counter-intuitive as they define semantics by what-they-are-not; and should be replaced by generative classifiers which define semantics by what-they-are. Unfortunately, generative classifiers are significantly less accurate. This may be caused by the tendency of generative models to focus on easy to model semantic generative factors and ignore non-semantic factors that are important but difficult to model. We propose a new generative model in which semantic factors are accommodated by shell theory's hierarchical generative process and non-semantic factors by an instance specific noise term. We use the model to develop a classification scheme which suppresses the impact of noise while preserving semantic cues. The result is a surprisingly accurate generative classifier, that takes the form of a modified nearest-neighbor algorithm; we term it distance classification. Unlike discriminative classifiers, a distance classifier: defines semantics by what-they-are; is amenable to incremental updates; and scales well with the number of classes.

MWPToolkit: An Open-Source Framework for Deep Learning-Based Math Word Problem Solvers

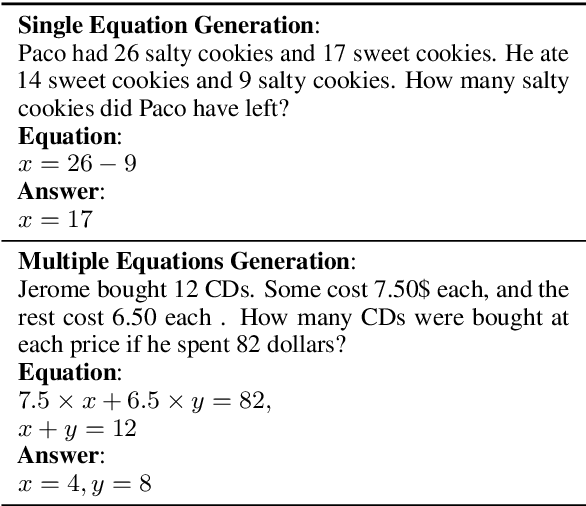
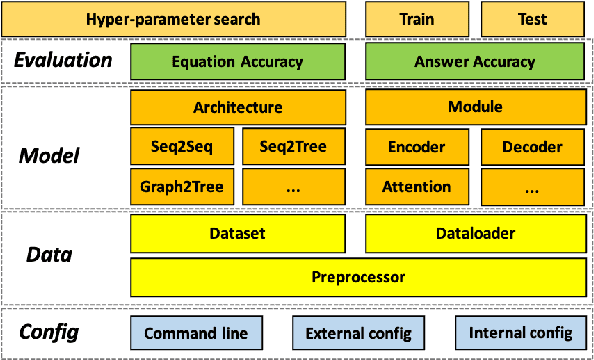
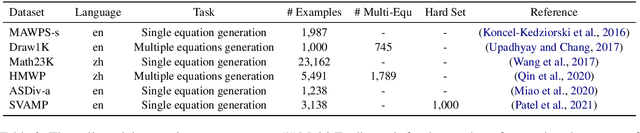
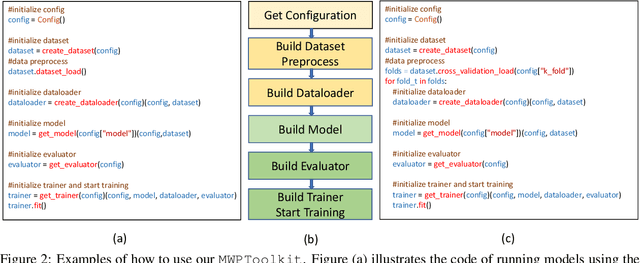
Developing automatic Math Word Problem (MWP) solvers has been an interest of NLP researchers since the 1960s. Over the last few years, there are a growing number of datasets and deep learning-based methods proposed for effectively solving MWPs. However, most existing methods are benchmarked soly on one or two datasets, varying in different configurations, which leads to a lack of unified, standardized, fair, and comprehensive comparison between methods. This paper presents MWPToolkit, the first open-source framework for solving MWPs. In MWPToolkit, we decompose the procedure of existing MWP solvers into multiple core components and decouple their models into highly reusable modules. We also provide a hyper-parameter search function to boost the performance. In total, we implement and compare 17 MWP solvers on 4 widely-used single equation generation benchmarks and 2 multiple equations generation benchmarks. These features enable our MWPToolkit to be suitable for researchers to reproduce advanced baseline models and develop new MWP solvers quickly. Code and documents are available at https://github.com/LYH-YF/MWPToolkit.

The Gap of Semantic Parsing: A Survey on Automatic Math Word Problem Solvers

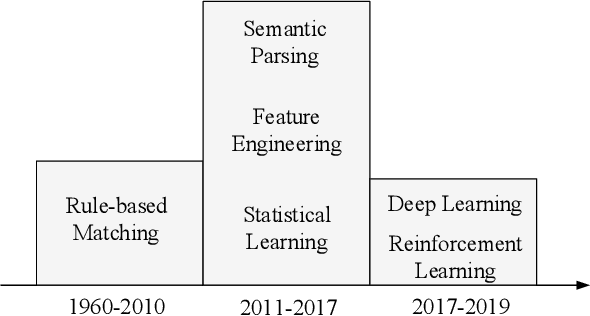
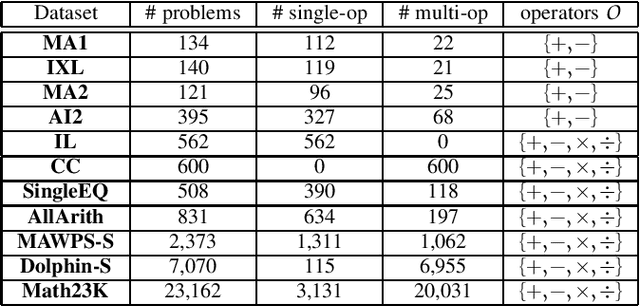
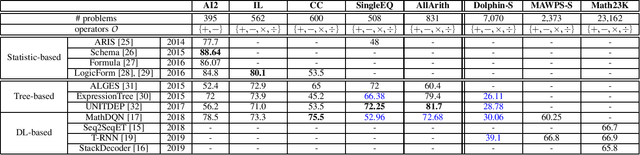
Automatically solving mathematical word problems (MWPs) is challenging, primarily due to the semantic gap between human-readable words and machine-understandable logics. Despite a long history dated back to the 1960s, MWPs has regained intensive attention in the past few years with the advancement of Artificial Intelligence (AI). To solve MWPs successfully is considered as a milestone towards general AI. Many systems have claimed promising results in self-crafted and small-scale datasets. However, when applied on large and diverse datasets, none of the proposed methods in the literatures achieves a high precision, revealing that current MWPs solvers are still far from intelligent. This motivated us to present a comprehensive survey to deliver a clear and complete picture of automatic math problem solvers. In this survey, we emphasize on algebraic word problems, summarize their extracted features and proposed techniques to bridge the semantic gap, and compare their performance in the publicly accessible datasets. We will also cover automatic solvers for other types of math problems such as geometric problems that require the understanding of diagrams. Finally, we will identify several emerging research directions for the readers with interests in MWPs.