Awni Altabaa
Unlocking Out-of-Distribution Generalization in Transformers via Recursive Latent Space Reasoning
Oct 15, 2025Abstract:Systematic, compositional generalization beyond the training distribution remains a core challenge in machine learning -- and a critical bottleneck for the emergent reasoning abilities of modern language models. This work investigates out-of-distribution (OOD) generalization in Transformer networks using a GSM8K-style modular arithmetic on computational graphs task as a testbed. We introduce and explore a set of four architectural mechanisms aimed at enhancing OOD generalization: (i) input-adaptive recurrence; (ii) algorithmic supervision; (iii) anchored latent representations via a discrete bottleneck; and (iv) an explicit error-correction mechanism. Collectively, these mechanisms yield an architectural approach for native and scalable latent space reasoning in Transformer networks with robust algorithmic generalization capabilities. We complement these empirical results with a detailed mechanistic interpretability analysis that reveals how these mechanisms give rise to robust OOD generalization abilities.
CoT Information: Improved Sample Complexity under Chain-of-Thought Supervision
May 21, 2025
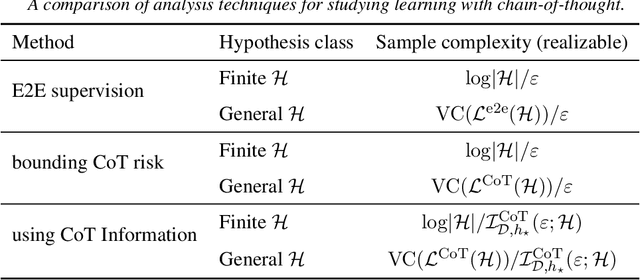
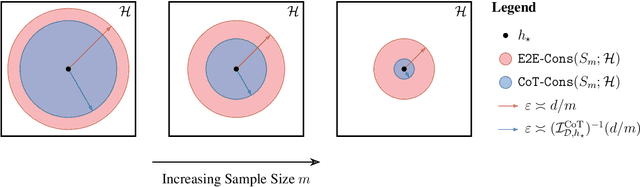

Abstract:Learning complex functions that involve multi-step reasoning poses a significant challenge for standard supervised learning from input-output examples. Chain-of-thought (CoT) supervision, which provides intermediate reasoning steps together with the final output, has emerged as a powerful empirical technique, underpinning much of the recent progress in the reasoning capabilities of large language models. This paper develops a statistical theory of learning under CoT supervision. A key characteristic of the CoT setting, in contrast to standard supervision, is the mismatch between the training objective (CoT risk) and the test objective (end-to-end risk). A central part of our analysis, distinguished from prior work, is explicitly linking those two types of risk to achieve sharper sample complexity bounds. This is achieved via the *CoT information measure* $\mathcal{I}_{\mathcal{D}, h_\star}^{\mathrm{CoT}}(\epsilon; \calH)$, which quantifies the additional discriminative power gained from observing the reasoning process. The main theoretical results demonstrate how CoT supervision can yield significantly faster learning rates compared to standard E2E supervision. Specifically, it is shown that the sample complexity required to achieve a target E2E error $\epsilon$ scales as $d/\mathcal{I}_{\mathcal{D}, h_\star}^{\mathrm{CoT}}(\epsilon; \calH)$, where $d$ is a measure of hypothesis class complexity, which can be much faster than standard $d/\epsilon$ rates. Information-theoretic lower bounds in terms of the CoT information are also obtained. Together, these results suggest that CoT information is a fundamental measure of statistical complexity for learning under chain-of-thought supervision.
Disentangling and Integrating Relational and Sensory Information in Transformer Architectures
May 26, 2024



Abstract:The Transformer architecture processes sequences by implementing a form of neural message-passing that consists of iterative information retrieval (attention), followed by local processing (position-wise MLP). Two types of information are essential under this general computational paradigm: "sensory" information about individual objects, and "relational" information describing the relationships between objects. Standard attention naturally encodes the former, but does not explicitly encode the latter. In this paper, we present an extension of Transformers where multi-head attention is augmented with two distinct types of attention heads, each routing information of a different type. The first type is the standard attention mechanism of Transformers, which captures object-level features, while the second type is a novel attention mechanism we propose to explicitly capture relational information. The two types of attention heads each possess different inductive biases, giving the resulting architecture greater efficiency and versatility. The promise of this approach is demonstrated empirically across a range of tasks.
On the Role of Information Structure in Reinforcement Learning for Partially-Observable Sequential Teams and Games
Mar 01, 2024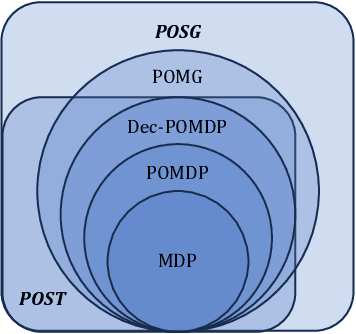
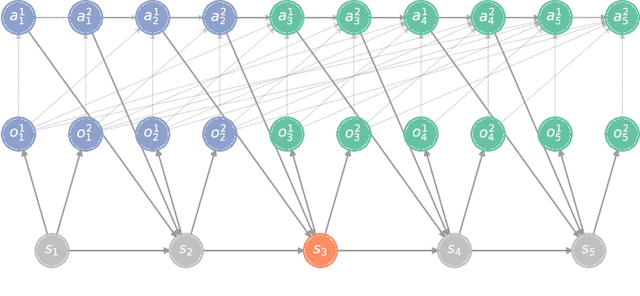
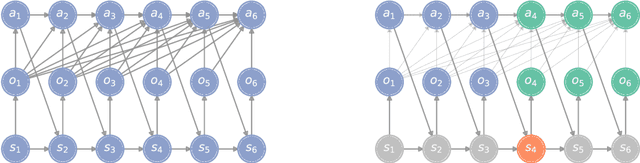
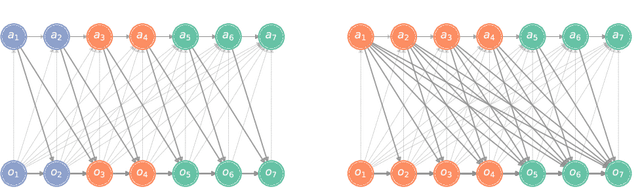
Abstract:In a sequential decision-making problem, the information structure is the description of how events in the system occurring at different points in time affect each other. Classical models of reinforcement learning (e.g., MDPs, POMDPs, Dec-POMDPs, and POMGs) assume a very simple and highly regular information structure, while more general models like predictive state representations do not explicitly model the information structure. By contrast, real-world sequential decision-making problems typically involve a complex and time-varying interdependence of system variables, requiring a rich and flexible representation of information structure. In this paper, we argue for the perspective that explicit representation of information structures is an important component of analyzing and solving reinforcement learning problems. We propose novel reinforcement learning models with an explicit representation of information structure, capturing classical models as special cases. We show that this leads to a richer analysis of sequential decision-making problems and enables more tailored algorithm design. In particular, we characterize the "complexity" of the observable dynamics of any sequential decision-making problem through a graph-theoretic analysis of the DAG representation of its information structure. The central quantity in this analysis is the minimal set of variables that $d$-separates the past observations from future observations. Furthermore, through constructing a generalization of predictive state representations, we propose tailored reinforcement learning algorithms and prove that the sample complexity is in part determined by the information structure. This recovers known tractability results and gives a novel perspective on reinforcement learning in general sequential decision-making problems, providing a systematic way of identifying new tractable classes of problems.
Approximation of relation functions and attention mechanisms
Feb 13, 2024Abstract:Inner products of neural network feature maps arises in a wide variety of machine learning frameworks as a method of modeling relations between inputs. This work studies the approximation properties of inner products of neural networks. It is shown that the inner product of a multi-layer perceptron with itself is a universal approximator for symmetric positive-definite relation functions. In the case of asymmetric relation functions, it is shown that the inner product of two different multi-layer perceptrons is a universal approximator. In both cases, a bound is obtained on the number of neurons required to achieve a given accuracy of approximation. In the symmetric case, the function class can be identified with kernels of reproducing kernel Hilbert spaces, whereas in the asymmetric case the function class can be identified with kernels of reproducing kernel Banach spaces. Finally, these approximation results are applied to analyzing the attention mechanism underlying Transformers, showing that any retrieval mechanism defined by an abstract preorder can be approximated by attention through its inner product relations. This result uses the Debreu representation theorem in economics to represent preference relations in terms of utility functions.
Relational Convolutional Networks: A framework for learning representations of hierarchical relations
Oct 05, 2023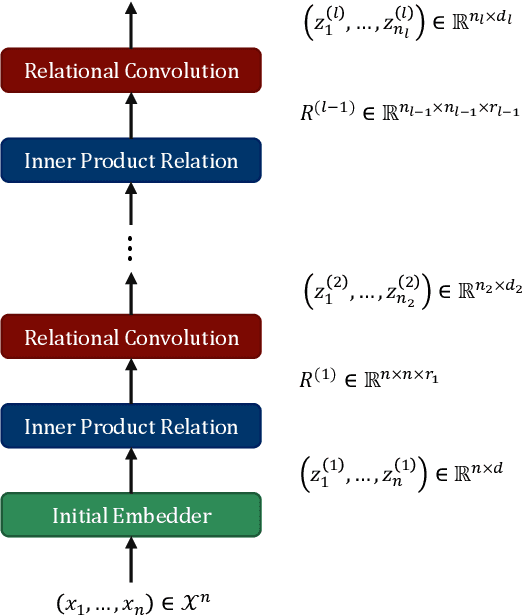

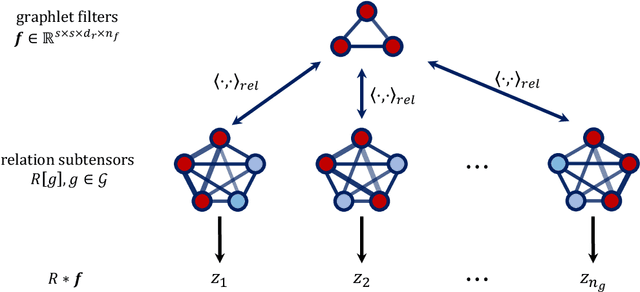

Abstract:A maturing area of research in deep learning is the development of architectures that can learn explicit representations of relational features. In this paper, we focus on the problem of learning representations of hierarchical relations, proposing an architectural framework we call "relational convolutional networks". Given a sequence of objects, a "multi-dimensional inner product relation" module produces a relation tensor describing all pairwise relations. A "relational convolution" layer then transforms the relation tensor into a sequence of new objects, each describing the relations within some group of objects at the previous layer. Graphlet filters, analogous to filters in convolutional neural networks, represent a template of relations against which the relation tensor is compared at each grouping. Repeating this yields representations of higher-order, hierarchical relations. We present the motivation and details of the architecture, together with a set of experiments to demonstrate how relational convolutional networks can provide an effective framework for modeling relational tasks that have hierarchical structure.
The Relational Bottleneck as an Inductive Bias for Efficient Abstraction
Sep 12, 2023

Abstract:A central challenge for cognitive science is to explain how abstract concepts are acquired from limited experience. This effort has often been framed in terms of a dichotomy between empiricist and nativist approaches, most recently embodied by debates concerning deep neural networks and symbolic cognitive models. Here, we highlight a recently emerging line of work that suggests a novel reconciliation of these approaches, by exploiting an inductive bias that we term the relational bottleneck. We review a family of models that employ this approach to induce abstractions in a data-efficient manner, emphasizing their potential as candidate models for the acquisition of abstract concepts in the human mind and brain.
Abstractors: Transformer Modules for Symbolic Message Passing and Relational Reasoning
Apr 01, 2023



Abstract:A framework is proposed that casts relational learning in terms of transformers, implementing binding between sensory states and abstract states with relational cross attention mechanisms.
Decentralized Multi-Agent Reinforcement Learning for Continuous-Space Stochastic Games
Mar 16, 2023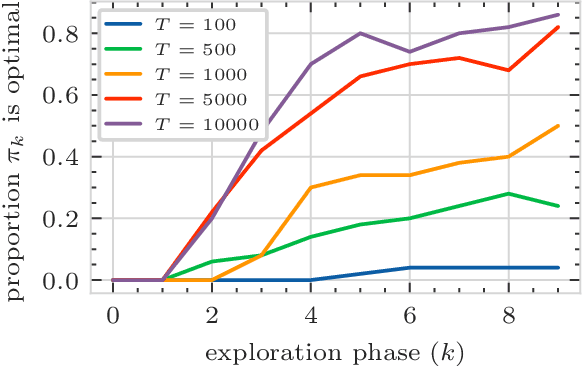
Abstract:Stochastic games are a popular framework for studying multi-agent reinforcement learning (MARL). Recent advances in MARL have focused primarily on games with finitely many states. In this work, we study multi-agent learning in stochastic games with general state spaces and an information structure in which agents do not observe each other's actions. In this context, we propose a decentralized MARL algorithm and we prove the near-optimality of its policy updates. Furthermore, we study the global policy-updating dynamics for a general class of best-reply based algorithms and derive a closed-form characterization of convergence probabilities over the joint policy space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge